Kollegstufenjahrgang 2000/2002
F A C H A R B E I T
aus dem Fach
MATHEMATIK
Der Rechenschieber – mathematischer Hintergrund, Geschichte, Anwendung
Verfasser: Gerhard Bumes
Inhalt:
0. Die „Vorgeschichte“ dieser Arbeit
I. Der Rechenschieber – ein „praktisches Rechenhilfsmittel“(1) unserer Vorfahren!?
II. Von der Entdeckung des Logarithmus zum Rechenschieber
1. John Napier als „Erfinder“ des Logarithmus
2. Die Gunterskala
3. Die ersten „richtigen“ Rechenschieber: Körper und Zunge
III. Rechenregeln und Rechenbeispiele
1. Die Skalen A, B, C, D: Multiplikation, Division, Proportionen, Quadrate, Wurzeln
2. Geometrische Berechnungen: Sinus, Kosinus, Tangens und Kreisberechnungen
3. Ausblick: Lösen von quadratischen Gleichungen, Log-Log Skalen
IV. Der Rechenschieber als Gebrauchsgegenstand
1. 17. bis 19. Jahrhundert: Rechengerät der Gelehrten
2. Die „deutsche Periode“ ab 1872: Rechenschieber für die Masse
V. Rechenschieber als Sammelobjekt
Quellenverzeichnis
0. Die „Vorgeschichte“ dieser Arbeit
Warum beschäftigt sich ein Schüler mit Rechenschiebern? Das wird sich wahrscheinlich jeder Leser zu Beginn fragen. Deshalb möchte ich kurz darauf eingehen:
In Bayern ist jeder Schüler in der 12. bzw. 13. Klasse verpflichtet, eine eigenständig angefertigte Facharbeit zu einem von ihm gewählten Thema zu verfassen. Da mir die im Fach Mathematik vorgeschlagenen Aufgabenstellungen nicht sehr gefielen, machte ich mich im Internet auf die Suche nach einem interessanteren Stoffgebiet. Obwohl mir der Begriff „Rechenschieber“ praktisch nichts sagte und mich vor allem deshalb neugierig machte, einigte ich mich mit meinem Lehrer auf dieses Thema. Nach einigen Gesprächen mit älteren Lehrern und Bekannten, die den Umgang mit dem Rechenstab noch in ihrer Schulzeit erlernt haben, ersteigerte ich einen VEB Mantissa-Rechenschieber bei ebay, um auch die Praxis nicht zu kurz kommen zu lassen. Weil meine Materialien zu dieser Zeit noch ziemlich dürftig waren, versuchte ich im Internet an Informationen zu kommen. Bei diesen Nachforschungen stieß ich zufällig auf die Seite des IM. Da ich nicht weit von München entfernt wohne, entschloss ich mich bald, auf dieses Treffen zu fahren. Dies stellte sich als echter Glücksgriff heraus: Ich konnte dort nicht nur Materialen zu meinem Thema sammeln, sondern vor allem auch einige Sammler kennenlernen, die mir bei meiner Arbeit sehr viel weitergeholfen haben. Für diese Hilfsbereitschaft bin ich äußerst dankbar, da sie mir jede Menge Zeit und Ärger erspart hat. Umso mehr bin ich natürlich glücklich und stolz, dass meine Arbeit jetzt auf dieser Seite zu lesen ist, durch die alles seinen Anfang nahm…..
I. Der Rechenschieber – ein „praktisches Rechenhilfsmittel“(1) unserer Vorfahren!?
Um 1820 wird aus England Folgendes berichtet: Es wird „(…) kein Beinkleid verfertigt, ohne einen eigenen Sack hineinzunähen, der bloß für das Tragen des „sliding rule“ bestimmt ist (…)“(2).
Unvorstellbar im 21. Jahrhundert! Oder doch nicht? Eine ganz ähnliche Tatsache kann man auch in unserer Zeit beobachten: Welche Jacke hat sie nicht, die Tasche zum Verstauen des Handys? Wenn man das Zitat aus diesem Blickwinkel betrachtet, dürfte es leichter zu verstehen sein; es gab wirklich eine Zeit in der der Rechenschieber ein alltäglicher Gebrauchsgegenstand war, genau wie in unserer Zeit das Handy.
Aber woher kommt es dann, dass diese Rechenhilfe für Multiplikation, Division oder Potenzberechnungen heutzutage beinahe keiner mehr kennt? Der Rechenschieber ist überholt, daran soll in dieser Arbeit nicht gezweifelt werden. Der Aufschwung der digitalen Hilfsmittel wie Taschenrechner und PC hat ihn verdrängt. Auch zurecht, die Vorteile der modernen Geräte sind offensichtlich: Einfachere Bedienung, Schnelligkeit und größere Genauigkeit.
Dennoch ist der Rechensstab, wie er von einigen auch genannt wird, eine nähere Betrachtung wert: Zum Einen aufgrund seines einfachen Grundprinzips, das auf dem Logarithmus basiert, zum Anderen aufgrund seiner Anwendung. Viele Generationen von Mathematikern, Physikern und Ingenieuren haben ihn für Berechnungen und Konstruktionen verwendet, was ihm eine Position als „Statussymbol“ einbrachte.

Vergangenheit: Rechenschieber als Statussymbol für den „Mann von Welt“
Quelle: http://amug.org/~puppy/
Deshalb soll im Folgenden die Geschichte des „sliding rule“ (auch „slide rule“) von seinen Anfängen im 17. Jahrhundert bis zu seinem „bitteren Ende“ in den 70er Jahren des 20. Jahrhunderts dargestellt werden.
II. Von der Entdeckung des Logarithmus zum Rechenschieber
1. John Napier als „Erfinder“(3) des Logarithmus
Schottland, 16. Jahrhundert: Wissenschaftliches „Sumpfland“ ist die wohl treffendste Bezeichnung. In diese Zeit wurde John Napier, Baron von Merchiston (heute Stadtteil von Edinburg), im Jahre 1550 geboren. In seiner Jugend und frühen Erwachsenenzeit widmete er sich aktuellen politisch-religiösen Themen: Als bekennender Protestant verfasste er mehrere Schriften gegen die „Papisten“, z.B. „A Plaine Discovery of the Whole Revelation of St. John.“(4), in denen er auch eine gewisse poetische Ader zu erkennen gibt. Außerdem beschäftigte sich Napier (oder „Nepero“, „Neper“, „Naper“, „Nepair“(5), wie der Name bisweilen geschrieben wird) auch mit Düngemitteln für den Ackerbau und erfand verschiedene Kriegsgeräte.

John Napier (1550-1617)
Quelle: http://www-ppg.dcs.st-and.ac.uk/Languages/Napier88/JohnNapier/
Seine genialste Erfindung jedoch ist auf dem Gebiet der Mathematik zu suchen: Nachdem er sich – wahrscheinlich unter anderem bei einem Besuch in Frankreich – Grundkenntnisse angeeignet hatte, machte er selber Entdeckungen. Bereits um 1594 soll er die Hauptgedanken des Logarithmus gefunden haben; formuliert hat er sie schließlich 1614 in seinem wohl wichtigsten Werk „Mirifici Logarithmorum Canonis Descriptio“(6).

Titelblatt der „Descriptio“
Quelle: http://www-history.mcs.st-andrews.ac.uk/history/Bookpages/Napier10.jpeg
Das Werk besteht aus 30 Seiten Erklärungen und Hinweisen und anschließenden 90 Seiten Logarithmentafeln, die Napier selbst berechnete. Napier bezeichnet sich darin als „Erfinder“ („Inventore“)(3) der Logarithmen, was wirklich zutreffend ist. In der Schweiz brachte zwar Jost Bürgi (1552-1632) unabhängig von Napier 1620 ein ähnliches Werk („Arithmetische und Geometrische Progreß Tabulen“(7)) in deutscher Sprache heraus; der Preis der Erstveröffentlichung gebührt aber Napier. Die Logarithmen Bürgis fanden bald bei Kepler Verwendung, der mit Bürgi befreundet war; er benutzte sie zur Berechnung seiner astronomischen Gesetze.
Während heute im Allgemeinen die Logarithmenfunktionen als Umkehrfunktionen der Exponentialfunktionen beschrieben werden, begründete Napier seine „artificial numbers“(8), wie er sie zuerst nannte, auf ganz andere Weise. Er ging dabei von einer mehr anschaulich-geometrischen Herleitung aus (der Funktionsbegriff war zu seiner Zeit noch nicht gebräuchlich!), und verwendete deshalb auch keine Basis im heutigen Sinne(9):
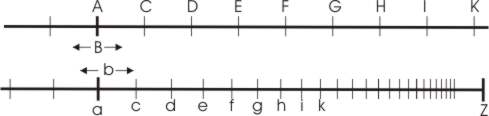
Er betrachtet die Strecke [aZ], die die Länge 10^6LE besitzen soll, und eine Gerade durch A, und lässt jeweils einen Punkt b bzw. B darauf „wandern“. Die Punkte C, D, E, F,…. sollen dabei die gleichen Abstände besitzen und von B in jeweils gleichen Zeitabständen delta t erreicht werden. Die Geschwindigkeit v des Punktes B ist also konstant. Der Punkt b dagegen besitzt ebenfalls die Anfangsgeschwindigkeit v, seine Geschwindigkeit nimmt aber proportional zur zurückgelegten Strecke ab, er erreicht aber die Punkte c, d, e, f,… ebenfalls in gleichen Zeitabständen delta t. Proportional (zur jeweiligen Ausgangsstrecke vor dem Zeitabschnitt delta t!) abnehmende Strecken heißt in diesem Fall:
__ __ __ __ __ __
ac : aZ = cd : cZ = de : dz = … = konst.
Er definiert dann den Logarithmus folgendermaßen:
__ __
log bZ = AB
Hierzu ein Beispiel:
t sei 3 * delta t:
B befindet sich zu diesem Zeitpunkt bei E, b bei e.
__ __
Also ist log eZ = AE.
Napier hat mit dieser Definition bereits wesentliche Grundzüge des Logarithmus erfasst. Der Definitionsbereich für die Streckenlänge , und damit für das Argument des Logarithmus, ist R+, da bei abnehmender Streckenlänge die Geschwindigkeit v ebenfalls kleiner wird und so Z nie erreicht werden kann. Man kann allerdings den Punkt b über a hinauswandern lassen, und damit Logarithmen von Zahlen, die größer sind als die Länge der Strecke [aZ], berechnen.
Hinsichtlich der Wertemenge zeigen sich aber einige Unterschiede zum „heutigen“ Logarithmus:
__ __ __
1. Formal gilt: bZ -> 0 => log = bZ = AB -> + unendlich ,
und ebenso:
__ __ __ __
für bZ > AZ => log bZ = AB < 0,
also wären die Vorzeichen genau entgegengesetzt zu den „heutigen“ Logarithmen mit einer Basis größer als 1. Diese Tatsache lässt Napier in den Logarithmentafeln allerdings außer Acht, da er nur Logarithmen von Zahlen berechnet die kleiner als (=10^6LE) sind und diesen ein positives Vorzeichen gibt.
2. Der Logarithmus der gesamten Strecke mit der von Napier festgelegten Länge 10^6 hat den Wert 0. Dies hat Napier aber später geändert, so dass sinnvollerweise log 1 = 0 gilt.
Auch die Rechengesetze leitet Napier in der „Descriptio“ her. In „Chapter II“(10) begründet er eine für den Rechenschieber fundamentale Regel: „The Logarithmes of Proportionall numbers and quantities are equally differing“(10). Er beweist dies anhand eines Beispiels, das in der Sprache der heutigen Mathematik etwa so ausgedrückt würde:
Behauptung:
__ __ __ __
cZ : eZ = hZ : kZ (I)
<=>
__ __ __ __
log cZ – log eZ = log hZ – log kZ (II)
Also führt er die Division auf eine Subtraktion der Logarithmen zurück!
Beweis:
nach seiner Definition gilt:
__ __ __ __
log cZ = AC; log eZ = AE; usw…
also ist Gleichung (II) gleichbedeutend mit:
__ __ __ __ __ __
AC – AE = AH – AK <=> – CE = – HK
Aus der Zeichnung ist ersichtlich, dass dies tatsächlich richtig ist und auch stimmen muss, da sich B mit konstanter Geschwindigkeit v bewegt.
Ein Kommentar sollte vielleicht noch zu den sich anschließenden Logarithmentafeln gemacht werden. Ebenso wie in der Darstellung der Logarithmen durch Strecken zeigt sich im Aufbau der Logarithmentafeln das geometrische Verständnis Napiers: Er berechnete in einem rechtwinkligen Dreieck mit einer Hypotenuse der Länge 10^6LE zu jeder Winkelsekunde den Sinuswert für einen Winkel und daraus die Länge der gegenüber liegenden Seite. Von dieser gibt er dann seinen Logarithmuswert an.

Logarithmentafeln aus der „Descriptio“
Quelle: http://www-math.sci.kun.nl/math/werkgroepen/gmfw/bronnen/napiertabellen.html
Wie Napier allerdings seine Werte berechnet hat, beschreibt er nicht in seinem Werk, vielleicht auch, um ein „Monopol“ für die Tafeln aufrechtzuerhalten. Die Berechnung ist für ihn nicht von Bedeutung, in erster Linie sind ihm die Vereinfachungen bei den verschiedensten Rechnungen wichtig, die ja durch den Logarithmus erreichbar sind.
Nach der Herausgabe der „Descriptio“ fand Napier bald reges Interesse in der damaligen wissenschaftlichen Welt von England. Ein Mathematikprofessor aus London, Henry Briggs (1561-1630)(11), machte Napier bei einem Besuch einige Verbesserungsvorschläge: Zum Einen gibt er den Anstoß, log 1 = 0 zu setzen, zum Anderen legt er auch log 10 = 1 fest. Damit erhält der Logarithmus die Basis 10, und wird deshalb „dekadischer“ oder – zu Ehren seines Erfinders – „Brigg´scher“ Logarithmus genannt. Für diesen gab Briggs 1624 auch eine Logarithmentafel („Arithmetica Logarithmica“(12)) heraus. Napier selbst verfasste noch zwei weitere Schriften: In der „Rabdologia“ beschreibt er eine nicht-logarithmische Multiplikationshilfe, die sog. „Napier´s bones“ oder „numbering rods“(13). Im anderen Werk, „Mirifici Logarithmorum Canonis Constructio“(14), das gewissermassen eine „Fortsetzung“ zur „Descriptio“ darstellt, befasst er sich wiederum mit den Logarithmen; die „Constructio“ wurde aber erst 1620 herausgegeben und hat im Vergleich zu seinem ersten Werk wenig Bekanntheit erlangt. Napier starb am 3.April 1617 und konnte so den Triumphzug „seiner“ Logarithmen nicht mehr miterleben.
2. Die Gunterskala
Edmund Gunter (1581-1626) war Professor für Astronomie in London und eng mit Henry Briggs befreundet. Er beschäftigte sich intensiv mit dessen Arbeit und erweiterte die Logarithmentafeln in seinem Werk „Canon Triangulorum“(15) durch Logarithmen von anderen Sinus- und Tangenswerten. Außerdem hatte er 1620 die Idee, die dekadischen Logarithmen als Strecken auf ein „Lineal“ abzutragen. Diese „Gunterscale“(16), wie das Gerät oft bezeichnet wird, war aus Buchsbaumholz und ca. 60cm lang. Der entscheidende Nachteil war natürlich, dass die Strecken mit einem Stechzirkel abgetragen werden mussten. Dennoch hatte der „Gunter“ einige Anhänger, vor allem bei Seefahrern(17), die den Umgang mit dem Stechzirkel ja gewohnt waren.
Das Prinzip der Gunterskala ist dasselbe wie das der späteren Rechenschieber und lässt sich durch Napier´s Regel (siehe II.1.) leicht erklären:
Es gelte: a:b = c:d
und damit lg a - lg b = lg c - lg d
Man setze b = 1, und damit lg b = lg 1 = 0
Also:
a:1 = a = c:d
<=>
lg a - lg 1 = lg a = lg c - lg d
und daraus folgt:
lg a = lg (c:d) = lg c - lg d
Man braucht also nur noch die berechneten Logarithmen in Strecken umzusetzen, und kann dann, durch Subtraktion dieser Strecken, den Quotienten der Argumente berechnen. Im Umkehrschluss können natürlich auch Produkte durch Addition der logarithmischen Strecken [lg (c•d) = lg c + lg d] berechnet werden.
Graphisch dargestellt würde das heißen, man trägt von einem Punkt A die Strecken (lg x)LE ab. An den Endpunkt schreibt man allerdings der Einfachheit halber nur die Zahl x, da ja der Logarithmus schon in den Strecken enthalten ist. Weil nach der Änderung durch Napier und Henry Briggs (lg 1) LE = 0 LE gilt, steht an der Stelle A also die Zahl 1.
Die Multiplikation würde graphisch folgendermaßen aussehen:
Beispiel: 5 * 10 = 50
Anwendung des Logarithmus:
lg (5*10) = lg 5 + lg 10
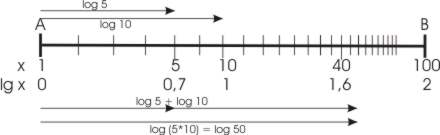
Der „Gunter“(18) und die ersten Rechenschieber hatten als Grundskala die „line of proportion“(19), von 1 – 100, mit der aber alle Produkte berechnet werden können (genaueres Abschnitt III). Außerdem wurde er durch eine Wurzel-Skala, verschiedene trigonometrische Skalen und eine Kuben-Skala ergänzt, wahrscheinlich durch Edmund Wingate (1596-1656).
Das umständliche Übertragen der Strecken durch den Stechzirkel wurde bald darauf, etwa um 1630, behoben: Entweder wiederum Wingate, oder aber der Landpfarrer und Mathematiker William Oughtred (1575-1660)(20), darüber herrschte bis zum Beginn des 20. Jahrhunderts keine Klarheit(21) (heute wird allerdings Oughtred diese Erfindung zugesprochen), verwendete zwei solcher Gunterskalen, die von Hand zusammengehalten werden mussten und verschob sie aneinander. Zur selben Zeit wurde auch die erste Rechenscheibe (vgl. V.) konstruiert, entweder ebenfalls von Oughtred oder aber von Delamain(22).
3. Die ersten „richtigen“ Rechenschieber
Der letzte Schritt zum eigentlichen Rechenschieber vollzog sich erstaunlich rasch: Ohne irgendwelche Zwischenentwicklungen konstruierte Robert Bissaker einen Rechenschieber, der folgende Aufschrift trägt: „Made by Robert Bissaker, 1654, for T.W.“(23) (wer mit T.W. gemeint ist, ist unbekannt).
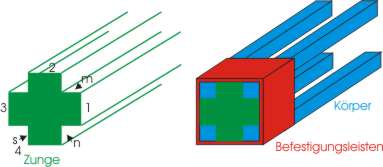
Rechenschieber von Robert Bissaker
nach: Horsburgh, Section F, Seite 164
Er war wie die Gunterskala ca. 60cm lang, und hatte, anders als die späteren Modelle, einen quadratischen Querschnitt. Von den 19 Skalen sind drei auf den Innenseiten der kreuzförmigen Zunge (s, n, m) und jeweils vier auf den Außenseiten (1,2,3,4) angebracht. Auf der Seite 1 sind z.B. drei logarithmische Skalen von 1-100 – zwei auf dem Körper und eine auf der Zunge – und eine Sinusskala aufgetragen. Durch die Verschiebbarkeit der Zunge wird die Multiplikation bzw. Division ermöglicht. Die anderen Seiten bestehen aus logarithmisch-geometrischen Skalen (Sinus, Tangens), die auch paarweise angeordnet und verschiebbar sind.
Eine Besonderheit dieses Rechenschiebers ist der „cursor“ oder „runner“(24) (Läufer): Er befindet sich zwischen den Befestigungsleisten (diese halten den Körper am Anfang und Ende zusammen) und weist ebenfalls einen quadratischen Querschnitt auf, ist aber im Gegensatz zu diesen nicht fest mit den vier Teilen des Körpers verbunden, sondern auf dem Körper verschiebbar. Der Läufer ist bei diesem Rechenschieber hauptsächlich wegen der Stabilität vorhanden, er bietet aber vor allem auch praktische Vorteile beim Rechnen, da durch ihn die Skalen verbunden werden; sie müssen deshalb nicht mehr genau gegenüber stehen, sondern können sogar auf verschiedenen Seiten liegen. Der Läufer konnte sich allerdings erst sehr viel später voll etablieren (Genaueres siehe IV.2).
Ein weiterer Name wird oft mit den frühen Rechenschiebern in Verbindung gebracht: Seth Partridge (1603-1686)(25). Er entwickelte 1657 einen Rechenschieber mit Skalen auf nur zwei statt auf vier Seiten, der als Urtyp des Doppelseiten-Rechenschiebers gilt. Fünf Jahre später wurde außerdem zum ersten Mal der Begriff „sliding rule“(26) von John Brown in einer Anleitung zu einem Rechenschieber verwendet.
III. Rechenregeln und Rechenbeispiele
Nach der Darstellung der Entwicklung des Rechenschiebers in seiner Urform folgt im nächsten Abschnitt eine Beschreibung verschiedener Rechenregeln, da erst mit diesem Hintergrundwissen die Funktionsweise und die Besonderheiten späterer Modelle deutlich und verständlich werden. Es können dabei nicht alle Funktionen aufgezeigt werden, sondern nur ausgewählte Beispiele, da sonst der Rahmen gesprengt würde. Als Modell wird der Rechenschieber Aristo Nr. 99 Rietz (Skalenlänge 25cm) verwendet; selbstverständlich können die Rechenwege aber auch auf andere Modelle mit ähnlicher Skalenanordnung übertragen werden.
Vorderseite:

Quelle: http://www.tcocd.de/Pictures/SlideRules/Aristo/nr99.html
K: Kubenskala x^3
A (auf dem Körper), B (auf der Zunge): Quadratskala x^2 von 1-100,
wobei die Entfernung von 1-10 gleich der Entfernung von 10-100
(log 100 = log 10^2 = 2 log 10)
D (auf dem Körper), C (auf der Zunge): Skala x
Unterteilung:
von 1 bis 2: 1 Teilstrich entspricht 1
von 2 bis 4: 1 Teilstrich entspricht 2
von 4 bis 10: Teilstrich entspricht 5
CI, bei einigen Modellen auch BI (auf der Zunge):
Reziprokskala 1/x bzw. 1/x^2 (rot!)
L (auf dem Körper): Mantissenskala lg x (Zehnerlogarithmus)
Rückseite:

Quelle: http://www.tcocd.de/Pictures/SlideRules/Aristo/nr99.html
S: Skala für Sinus von 5° bis 90°, Kosinus (90° – Sinus x) von 0° bis 85°
ST: Skala für Sinus, Tangens (Kleinwinkelnäherung sin = cos = tan) von 30´ bis 6°
T: Skala für Tangens von 5° bis 45° und von 45° bis 85°
Diese drei Skalen befinden sich auf der Zunge, die bei Bedarf auch umgedreht werden kann, so dass diese drei Skalen auf der Vorderseite und C, CI, BI, B auf der Rückseite sind.
Im Körperboden befinden sich außerdem zwei rote „Indexstriche“(27) auf Höhe der 1 bzw. 10 der Skala D. Durch diese Linie werden also die rückseitigen Skalen mit denen auf der Vorderseite in Verbindung gebracht.
Ein weiterer Teil dieses Rechenschiebers ist ein Klarsichtläufer, der über die ganze Länge verschoben werden kann. Er hat einen durchgezogenen Mittelstrich, links davon in der Entfernung (pi/4)^-1 einen Strich über die Skalen A, B, BI und einen Strich zur Umrechnung von kW in PS rechts davon. Rechts unten (über den Skalen C und D) befindet sich eine weitere Markierung, mit der Bedeutung (pi/4)^-0,5 (für Kreisberechnungen).
Eine Besonderheit gibt es noch beim Ablesen der Skalenstriche: Der Skalenteilungsstrich 2,66 bedeutet nämlich nicht nur diese Zahl, sondern ebenso 26,6 oder 266 oder 2660 oder 0,266. Es ist deshalb immer eine gedankliche Überschlagsrechnung notwendig, um die Größenordnung des Ergebnisses herauszufinden. Es werden dabei die Mantissen(28), auf drei oder vier Stellen genau (je nach Ablesebereich), von den Kennzahlen abgetrennt, und nur mit diesen die Rechnung ausgeführt; die Zehnerpotenzen (Kennzahlen) werden dann, miteinander verrechnet, einfach wieder an das Ergebnis angehängt.
1. Die Skalen A, B, C, D: Multiplikation, Division, Proportionen, Quadrate, Wurzeln
Die einfachste und zugleich ursprünglichste Rechenart mit dem Rechenschieber (vgl. Gunterskala) ist die Multiplikation bzw. Division. Nach Napier´s Formel (log (c*d) = log c + log d, siehe Seite 6 und 8/9) werden einfach die logarithmischen Strecken aneinander addiert. Dies kann man entweder mit den Skalen A und B oder mit den Skalen C und D ausführen. Bei der zweiten Variante ist natürlich die Ablesegenauigkeit größer, da die gesamte Länge auf diesen Skalen für die Zahlen von 1 bis 10, bei den Skalen A und B dagegen für die Zahlen von 1-100 genutzt wird.
Beispiel: 234567 * 33333
Die Stellenzahl dieser Werte geht weit über die Genauigkeit des Rechenschiebers hinaus, deshalb müssen die Zahlen zuerst auf eine gerundete Mantissenform gebracht werden:
234567 * 33333
= 2,346 * 10^5 * 3,33 * 10^4
= 2,346 * 3,33 * 10^9
Mit diesen Zahlen kann man die normale Streckenaddition durchführen, indem man die 1 der Skala C (Zunge) über die 2,346 auf Skala D bringt. Dann verschiebt man den Läufer so weit, bis er über der 3,33 auf Skala C ist, und liest auf Skala D das Ergebnis ab.

Quelle: „Rechenschieber“, Version 3.2
Das genaue Ergebnis ist 7818821811, das Ergebnis aus den gerundeten Zahlen 7,81218 * 10^9 (relativer Fehler 0,085%); aufgrund der Ablesegenauigkeit kann man aber höchstens 7,81 ablesen, was als Ergebnis 7,81 * 10^9 (rel. Fehler 0,113%) liefert.
Diese Schiebereinstellung kann natürlich auch zur Division von 7818821811 : 33333 verwendet werden. Die Reihenfolge der Schritte ist dann umgekehrt, man zieht die Strecken voneinander ab.
Eine Besonderheit der Skalen C und D ist das sogenannte „Durchschieben“(29) der Zunge: Als Beispiel kann 3 * 5 genannt werden. Bei dieser Rechnung befindet sich die 5 auf Skala C rechts außerhalb der 10 der Skala D, da log (3 * 5) = log 15 > log 10 (die Skala reicht ja nur bis 10!). Deshalb schiebt man die Zunge so lange nach links, bis die 10 (nicht wie vorher die 1) der Skala C über der 5 der Skala D steht. Dann liest man auf Skala D in „Koinzidenz“(30) (auf gleicher Höhe) zur 3 auf Skala C das Ergebnis – also 15 – ab.
Bei den Skalen A und B, mit denen man ebenfalls multiplizieren und dividieren kann, muss der Schieber nie durchgeschoben werden, da ihre Skalen bis 100 reichen und deshalb die Ergebnisse immer innerhalb der Skalen liegen.
Eine äußerst praktische Anwendung des Rechenschiebers ist das Berechnen von Verhältnissen. Vor allem bei Tabellenberechnungen oder maßstabsgetreuem Zeichnen können so nach einmaligem Einstellen verschiedene Werte abgelesen werden:
Beispiel: Maßstab 1:250, reale Längen: 50m, 66m, 85m, 23m
Lösung: Skala C-1 über Skala D-250 stellen, Läufer über D-50 (bzw. D-66, D-85) stellen, auf Skala C das Ergebnis ablesen (nach Überschlagsrechnung im Kopf!)
Bei 23m muss die Zunge wieder durchgeschoben werden.
Nach der Überschlagsrechnung erhält man folgende Ergebnisse:
50m := 20cm;
66m := 26,4cm;
84m := 33,6cm;
23m := 9,2cm
Mit den Skalen A und B können nicht nur Multiplikationen und Divisionen ausgeführt werden, sie dienen auch als Quadratskalen. Mit dem Läuferstrich kann zu jeder beliebigen Zahl auf der D-Skala das Quadrat auf der Skala A gefunden werden. Ebenso funktioniert dies mit den Skalen C und B. Als Umkehrung können natürlich auch Wurzeln gezogen werden; man stellt hier die Zahl auf der Skala A bzw. B ein und liest ihre Quadratwurzel auf Skala D bzw. C ab.
Außerdem gibt es noch die Kubenskala K, die die Zahlen von 1 bis 1000 trägt. Mit ihr können analog die dritten Potenzen oder die dritten Wurzeln zur Grundskala D berechnet werden.
Die beiden mittleren Skalen auf der Zunge, CI und BI, dienen der Kehrwertberechnung 1/x bzw. 1/x2. Durch sie kann außerdem eine Multiplikation mit x als Division durch 1/x (und auch umgekehrt) ausgedrückt werden, was in einigen Fällen Vorteile bringt.
2. Geometrische Berechnungen: Sinus, Kosinus, Tangens und Kreisberechnungen
Auf der Rückseite der Zunge befinden sich die drei Skalen S (Sinuswerte von 5° bis 90°), ST (Sinus- und Tangenswerte von 30´ bis 6°) und T (Tangenswerte von 5° bis 45°). Verschiebt man die Zunge so lange, bis unter einem der beiden roten „Indexstriche“(31) im Rechenschieberboden der Wert des Winkels steht, dessen trigonometrischer Funktionswert berechnet werden soll, kann man auf Skala C das Ergebnis ablesen. Dazu muss man den Rechenschieber umdrehen und über der 1 oder der 10 der Skala D – je nachdem, ob die Zunge nach links oder nach rechts hinausragt – den gesuchten Wert ablesen.
Obwohl keine Kosinusskala aufgezeichnet ist, lassen sich Kosinuswerte trotzdem ganz einfach bestimmen: Nach der Beziehung cos alpha = sin (90° – alpha) lässt sich der Kosinus in die Sinusfunktion umrechnen und so der Wert bestimmen.
Bei längeren Rechnungen mit diesen Skalen empfiehlt es sich allerdings, die Zunge umzudrehen, damit das ständige Wenden des Rechenschiebers nicht mehr erforderlich ist. Man liest dann die zugehörigen Funktionswerte einfach auf Skala D ab.
Beispiel (hier sind die trigonometrischen Skalen allerdings unter der Skala D dargestellt):
sin 8° = tan 7° 56´ = 0,1395 (= cos 82°)
und sin 48´ = cos 48´ = tan 48´ = 0,01395
(Achtung: für alpha < 5,5° => sin alpha ungefähr tan alpha < 0,1!)
Wie schon erwähnt trägt der Läufer eine kurze Marke links vom Mittelstrich über den Skalen A und B und ein rechts vom Mittelstrich über den Skalen C und D. Diese haben jeweils den Abstand (pi/4)^-1 von der langen Markierung in der Mitte, bzw. die Wurzel daraus (Kehrwert, da pi/4 nicht darstellbar auf dem schmalen Läufer).
Die beiden Striche haben folgende Bedeutung:
Formel für die Kreisfläche mit Durchmesser d als Variable:
A = r^2 * pi = d^2 : (pi/4)^-1
Man stellt auf Skala D mit dem Mittelstrich den Durchmesser d ein, und liest auf Skala A (d^2), allerdings unter dem linken Läuferstrich (Subtraktion der Strecke lg[(pi/4)^-1]), die Fläche ab. Ebenso kann man den rechten unteren Strich über den Durchmesser auf D stellen und unter dem Mittelstrich auf A ablesen. Dabei wird nur die Reihenfolge der Rechenschritte umgedreht, also zuerst durch (pi/4)^-0,5 dividiert und dann erst quadriert.
Umfangsberechnungen lassen sich ebenfalls mit dem Rechenschieber ausführen; dazu ist auf den vier Grundskalen A, B, C, D jeweils eine Marke pi eingetragen.
3. Ausblick: lg x – Skala, Lösen von quadratischen Gleichungen
Die unterste Skala auf dem Körper des Aristo Nr. 99 Rietz ist die Skala L zur Berechnung des Zehnerlogarithmus einer Zahl. Im Folgenden sollen nur die Regeln dieser Berechnung kurz gezeigt werden, ein Beweis würde zu weit führen.
Die Skala L ist im Gegensatz zu den anderen Skalen gleichmäßig von 0 bis 1 eingeteilt. Ein Teilstrich bedeutet dabei 0,002.
Beispiel: lg 45 = 1,653
wobei 45 als Numerus,
1 als Kennzahl
653 als Mantisse (andere Wortbedeutung als in III.!!)
bezeichnet wird.
Auf Skala L kann nur die Mantisse des Logarithmus einer Zahl (z.B. 45) auf Skala D abgelesen werden. Die Kennzahl wird nach folgender Regel bestimmt:
Für Numerus > 1 gilt: Kennzahl = Stellenzahl des Numerus (links vom Komma) – 1
Beispiele: Numerus: 3,8 38 38000
Kennzahl: 0,.. 1,.. 4,.. (32)
Für Zahlen mit Numerus < 1 gibt es ebenfalls eine (etwas kompliziertere) Regel, die hier nicht mehr aufgeführt werden soll. Außerdem ermöglicht die Skala L, ähnlich den Exponentialskalen (vgl. IV.1.), Potenzieren und Radizieren mit beliebigen Zahlen, allerdings etwas umständlicher.
Eine weitere Verwendung des Rechenschiebers ist das Lösen von quadratischen Gleichungen. Newton (vgl. Kap. IV.1) hat bereits eine ähnliche Methode entdeckt, und sogar mit kubischen Gleichungen durchgeführt. Das Verfahren beruht auf dem Satz von Vieta.
Gegeben sei eine quadratische Gleichung der Form x^2 + a x + b = 0
nach Satz von Vieta(33): x1 *x2 = b x1 + x2 = – a
und daraus: x1 + b/x1 = – a
Man stellt dann den Wert b auf CI über 1 auf D und versucht dann mit dem Läuferstrich je einen Wert auf CI und D zu finden, die sich gegenüberstehen, so dass die Summe dieser beiden -a ergibt. Man muss dabei besonders auf die Vorzeichen der beiden Lösungen achten, die entweder aus einer Tabelle zu entnehmen sind, oder durch Probieren bestimmt werden müssen.(34)
Ob dieses doch ziemlich umständliche Verfahren in der Praxis recht oft Verwendung fand, lässt sich heute schwer sagen. Es soll nur verdeutlichen, dass mit dem Rechenschieber auch komplexere Probleme gelöst werden können.
IV. Der Rechenschieber als Gebrauchsgegenstand
1. 17. – 19. Jahrhundert: Rechengerät der Gelehrten
Bis man so technisch ausgefeilte Rechenschieber wie den im vorigen Kapitel vorgestellten Aristo Rietz Nr. 99 herstellen konnte, bedurfte es fast 300 Jahre. Die ersten Rechenschieber wurden, wie im II. Abschnitt erläutert, von Bissaker und Partridge in England erfunden, das auch in den nächsten Jahrzehnten noch Vorreiter auf diesem Gebiet blieb. Nach 1660 breitete sich der Rechenschieber in verschiedenen Modellen vor allem in der wissenschaftlichen Gesellschaft Englands aus: Isaac Newton (1643-1727) zum Beispiel beschreibt 1675 eine Lösungsmöglichkeit für kubische Gleichungen mit dem Rechenschieber. Dazu verwendet er drei logarithmische Skalen, die mit Hilfe eines „Haarstrich(s)“(35) in Beziehung zueinander gebracht werden.
In der Folgezeit wurden verschiedenste Spezialrechenschieber entwickelt, z.B. für die „Seefahrt“, den „Schiffbau“ oder für „Holzberechnungen“(36). Der Rechenschieber wurde in dieser Zeit dann auch in Frankreich populär und gelangte von dort erst nach Deutschland: Im Jahre 1699 soll Michael Scheffelt (1652-1720)(37) den ersten deutschen Rechenschieber gebaut haben, der dem von Bissaker ziemlich ähnlich war. Seine Ausbreitung ging aber nur langsam voran, da die Herstellung noch von Hand von geschickten Instrumentenbauern wie G.F. Brander (1713-1783)(38) (lebte in Augsburg) vorgenommen werden musste. Dies erklärt auch, dass sehr viele verschiedene Modelle existierten, da jeder Handwerker seine Eigenheiten hinzufügte.
Um 1770 wurde in England durch den „Soho-rule“(39) endlich ein Standard geschaffen: James Watt (1736-1819), der Erfinder der Dampfmaschine, verwendete bei seinen Berechnungen verschiedene Rechenschieber, musste aber immer wieder die schlechte Qualität dieser feststellen. So ließ er von seinen Angestellten einen einfachen Rechenschieber mit zwei Skalen auf dem Körper (A von 1-100, D von 1-10) und zwei auf der Zunge (B, C, jeweils von 1-100) herstellen.
Auch hinsichtlich der Skalen wurden Fortschritte gemacht: So erfand z.B. Everard 1755 die Reziprokskala CI, die sich bald durchsetzte und auf den meisten Modellen aufgedruckt wurde.
Um mehrere Skalen auf einen Rechenschieber zu bringen, wurden auch verschiedenen Mehrschiebersysteme auf den Markt gebracht. Diese Entwicklung konnte aber später wieder eingedämmt werden: 1775 entwickelt John Robertson (1712-1776)(40) einen mechanischen Läufer, der sich allerdings erst 75 Jahre später voll etablieren konnte. Durch diesen konnten auch nicht aneinander liegende Skalen in Verbindung gebracht werden, was mehrere Zungen überflüssig machte.
1815 wurde von Roget eine neue Skalenordnung vorgestellt, die sich als sehr praktisch erwies. Die „doppellogarithmischen Skalen“(41) (Log-Log-Skalen) geben, wie der Name schon sagt, den Logarithmus vom Logarithmus an. Aufgrund ihrer Verwendung werden sie auch Exponentialskalen genannt, da man mit ihnen jede Art von Exponentialrechnungen durchführen kann:
Man betrachte: a^c = b
Anwendung des dekadischen Logarithmus:
c * lg a = lg b
nochmalige Anwendung des Logarithmus:
lg (c * lg a) = lg (lg b)
Logarithmusregel:
lg c + lg (lg a) = lg (lg b)
Es wird also eine Potenzierung/Radizierung auf eine Addition zurückgeführt, die durch Streckenaddition graphisch leicht umsetzbar ist. Dabei wird die Basis auf der Exponentialskala, der Exponent auf der Grundskala (C) und das Ergebnis wiederum auf der Exponentialskala abgelesen. Allerdings bedeutet auf diesen Skalen jeder Teilstrich eine bestimmte Zahl, nicht wie bei allen anderen Skalen nur die Mantisse. Deshalb wurden später auch drei LL-Skalen (oder mehr) auf den Rechenschiebern aufgebracht:
z.B.: LL1 von 1,010 bis 1,11
LL2 von 1,10 bis 3,0
LL3 von 2,5 bis 50000
Ab 1821 wurde auch der Einfluss der Industrialisierung spürbar. In Frankreich wurden durch die Firma Lenoir die ersten Rechenschieber, vor allem aus Holz, maschinell gefertigt. Dies war möglich, da bereits 1773 von Jesse Ramsden (1735-1800) eine „Längen-Teilmaschine“(42) konstruiert worden war, mit der man die Skalen einfacher einritzen konnte.
In Frankreich wurde dann auch das erste Skalensystem erfunden, das sich weithin durchsetzen konnte. Amédée Mannheim (1831-1906) erfand 1850 mit nur 19 Jahren das System Mannheim(43). Er verwendete die Skalen A und B von 1 bis 100 an der oberen, und die Skalen C und D von 1-10 an der unteren Gleitfuge. Auf der Rückseite des Schiebers war jeweils ein Sinus- und eine Tangensskala angebracht.
Das Besondere ist aber die Verwendung eines Läufers. Obwohl er unbewusst schon von Bissaker eingesetzt wurde, Newton ihn bewusst erwähnte („hairline“) und auch Robertson auf ihn hinwies, konnte er sich bis zu dieser Zeit nicht voll etablieren. Mit dem System Mannheim wurde der Läufer populär, und fand schon bald auf den meisten Rechenschiebermodellen Verwendung.
2. Die „deutsche Periode“(44) ab 1872: Rechenschieber für die Masse

Rechenschieber im Schulgebrauch (Werbegrafik von Dennert&Pape)
Quelle: http://www.hh.schule.de/metalltechnik-didaktik/users/luetjens/rechenschieber/schule/rs10.htm
Auch in Deutschland erkannte man die Vorteile des Rechenschiebers, nachdem in den meisten Nachbarländern ab ca. 1850 das Rechnen mit dem Rechenschieber sogar schon an Schulen empfohlen wurde und immer weitere Verbreitung fand(45). Da der Import aus Frankreich zu den Kriegszeiten nicht gerade günstig war, wurden bald Firmen gegründet, die die Rechenschieberproduktion ins Inland holten. Die in Hamburg-Altona ansässige Firma Dennert&Pape (später bekannt unter dem Markennamen „Aristo“) wurde zwar schon 1862 gegründet, ihr erster Rechenschieber wurde aber erst 10 Jahre später auf den Markt gebracht. Ein Konkurrent, nämlich Faber-Castell, begann mit der Rechenschieberproduktion in Stein bei Nürnberg 1892(46). Ein weiterer süddeutscher Hersteller dieser Zeit ist die Firma Nestler (gegründet 1878 in Lahr/Schwarzwald).
Aufgrund der industriellen Fertigung wurden immer wieder neue und bessere Modelle, aber auch Verfeinerungen an herkömmlichen Modellen erfunden und meist auch patentiert. Bereits 1886 presste Dennert&Pape weiße Celluloidfurniere(47) auf die Holzrechenschieber. Dies diente der Formstabilität und ebenso der Ablesegenauigkeit, hatte allerdings den Nachteil, dass die Farbe im Laufe der Jahre vergilbte. Auch die Form der Läufer wurde immer wieder weiterentwickelt. Die größte Neuerung wurde 1889 von Faber-Castell vorgestellt: Erstmals wurde ein Glasfenster in einem Rahmen verwendet, dessen Gleitfähigkeit durch eine Blattfeder erreicht wurde(48). Erstaunlicherweise hat sich aber bei der Länge der Geräte nicht allzu viel geändert: Es wurden Taschenmodelle, hauptsächlich mit 12,5 cm Skalenlänge, Normalmodelle (vor allem 25cm, aber auch 36 oder 40cm), und Büromodelle von 50, 60 oder 100cm hergestellt.
1902 wurde von Max Rietz (1872-1956) das „System Rietz“(49) erfunden, das vor allem bei Schulrechenschiebern sehr erfolgreich war. Auch der Aristo Nr. 99 Rietz (siehe III.) verwendet dieses Skalensystem. Neuartig war dabei die Kubenskala K auf der Vorderseite, ebenso die Mantissenskala L und später (ca. 1925) die Skalen CI und ST. Der Indexstrich im Boden wurde ebenfalls von ihm eingeführt. Bereits einige Jahre später wurde diese Skalenanordnung von dem Darmstädter Professor Alwin Walther (1898-1967)(50) nochmals erweitert; aufgrund seiner Herkunft wird es „System Darmstadt“ genannt. Er fügte die erwähnten Exponentialskalen (LL1, LL2, LL3) hinzu, was vor allem für technische und wissenschaftliche Rechnungen von Vorteil war. Es tauchten daneben noch einige andere Systeme auf, auch spezielle für bestimmte Berufsgruppen; erwähnt seien hier nur die Systeme „Perry“ und „Schweth“(51).
Obwohl viele der in Deutschland hergestellten Rechenschieber exportiert wurden, wurden auch in anderen Ländern verschiedene Rechenschieber-Firmen gegründet, z.B. Thornton in Manchester (RS-Herstellung ab 1895), Gamma in Ungarn (gegr. 1920) oder Graphoplex in Frankreich (Produktion ab 1941). Auch in Japan entstand 1895 eine bekannte Marke, nämlich Sun Hemmi. In Amerika machten sich früh eigene Entwicklungslinien bemerkbar: Die Firma Keuffel&Esser (gegr. 1867) importierte zunächst Rechenschieber (ab 1886), erlangte aber 1891 ein Patent für Doppelseitenrechenschieber, also einem Modell mit einem beide Seiten umfassenden Läufer, bei dem mehr Skalen aufgetragen und miteinander in Verbindung gebracht werden können. Dieser Aufbau wurde in Amerika ein durchschlagender Erfolg, in Deutschland wurden solche Typen („Duplex“ oder „Studio“-Modelle) erst nach dem 2. Weltkrieg produziert.
In Deutschland entwickelte sich unterdessen die Forschung hin zu anderen Materialien. Ab ca. 1930 wurden die meisten Modelle nicht mehr mit Celluloid beschichtet, sondern ganz aus Kunststoffplatten (PVC, Astralon(52)) ausgefräst. Vor dem Krieg hatte die Produktion dann einen Höchststand erreicht: Von der Firma Nestler, dem Marktführer in Deutschland zu dieser Zeit, wird berichtet, dass jährlich „über 1 Mio. Stück“(53) hergestellt wurden.
Obwohl durch den Krieg viele Maschinen zerstört waren oder danach demontiert wurden, konnte sich die Rechenschieberindustrie bald wieder emporarbeiten. Bei den meisten Firmen wurden bald die Kapazitäten aufgrund des guten Absatzes wieder gesteigert. So gründete Dennert&Pape (vertrieb ab 1936 Kunststoffrechenschieber unter dem Markennamen Aristo) 1951 im bayrischen Geretsried eine neue Fabrik, die innerhalb der nächsten sechs Jahre von sieben auf über 100 Mitarbeiter wuchs(54).
Anfang der 50er Jahre wurde bei den meisten Firmen schon das „Spritzgussverfahren“(55) eingesetzt, bei dem der Kunststoff einfach in einer Form aushärtete. Dieses Verfahren ermöglichte bald sogar das Gießen von Klarsichtläufern z.T. mit integrierter Vergrößerungslinse. Wie schon erwähnt, gewann in diesen Jahren auch der Doppelseitenrechenschieber immer mehr Bedeutung in Europa.
Diese „goldenen Jahre“ konnten aber nicht ewig dauern, wie abzusehen war. Nach dem Krieg wurde die Zukunft in den Industriestaaten auf dem Gebiet der Elektronik gesehen und so waren auch bald erste Erfolge zu verzeichnen: 1947 wurde bereits der erste Transistor erfunden, 1969 wurde mit Hilfe der integrierten Schaltung die erste elektronische Armbanduhr gebaut(56). Einige Rechenschieberproduzenten erkannten noch rechtzeitig die Tendenz und entwickelten ihrerseits elektronische Geräte (z.B. Sun-Hemmi ab 1967). Für die meisten war dies allerdings ein Ding der Unmöglichkeit, da die Produktionsstätten nicht auf diese neue Anforderung ausgelegt waren und Know-how und Kapital fehlte. Als dann ab 1972 die Taschenrechner immer billiger wurden, war das Ende des Rechenschiebers absehbar. Faber-Castell stellte in diesen Jahren noch Kombiprodukte vor, die auf der einen Seite einen Rechenschieber enthielten, auf der anderen einen elektronischen Taschenrechner. Diese Geräte konnten sich aber nicht recht durchsetzen, da ja die Taschenrechner bald so weit waren, dass sie die gleichen oder sogar mehr Funktionen hatten als die Rechenschieber, und noch dazu genauere Ergebnisse lieferten. Folgendes Zahlenbeispiel zeigt diesen rapiden Abstieg: Bei Dennert&Pape (Aristo) sank die Produktion 1974 auf 90%, 1975 auf 50% und 1976 sogar auf nur 27% der Herstellungsmenge von 1973(57). Die Folge war die Einstellung der Produktion, bei Dennert&Pape zum 31. Dezember 1976, bei Faber-Castell und vielen anderen etwa um die gleiche Zeit.
Einen „Vorteil“ hatten die Firmen in der DDR, dort nämlich konnte sich der Rechenschieber aufgrund des technologischen Rückstandes etwas länger behaupten. Meissner (gegr. 1932) wurde 1972 in einen Staatsbetrieb umgewandelt, in die VEB Mantissa („Volkseigener Betrieb“) und stellte bis 1984(58) verschiedene Schulmodelle (z.B. „Mono Rietz“) her. Dann aber war das endgültige Aus gekommen, der Rechenschieber geriet bei den meisten in Vergessenheit, nur noch einige Liebhaber und Sammler sind heute noch an diesem traditionsreichen Gerät interessiert.
V. Rechenschieber als Sammelobjekt
Wie mit allen Gebrauchsgegenständen, so ist es auch mit dem Rechenschieber: „If there is anything to collect, somebody will collect it!“(59) Aber warum ausgerechnet Rechenschieber? Vielleicht sollte man dazu einen Sammler selbst zu Wort kommen lassen. Eric R. Marcotte, ein kanadischer Sammler, „rechtfertigt“ sich auf seiner Homepage(60) so:
„For me, I guess slide rules carry with them a sense of nostalgia for earlier scientific times. When you use one, you get a much better feel for what numbers really mean than when you use a calculator or computer. They are remarkable technological instruments, built with precision and reliability in mind, and are as useable today as the day they were first made. Many are also intrinsically beautiful, with their celluloid covered wood, metal-framed glass cursors, and richly coloured leather cases. I didn’t set out to collect slide rules … but I find their incredible diversity and functionality amazing and intriguing.(…)“
Seit einiger Zeit gibt es auch Sammlervereinigungen, wie die „Oughtred-Society“(61) in den U.S.A., die regelmäßig Magazine herausgeben oder Treffen organisieren. So fand im September 2001 im Deutschen Museum das „7. Internationale Treffen für Rechenschieber- und Rechenmaschinensammler“ (IM) statt. Es wurde gemeinsam vom deutschen Sammlerring RST und der Oughtred Society organisiert. In einem umfangreichen Programm mit Vorträgen und der Aktion „Schüler treffen Sammler“ gab es auch die Möglichkeit, Rechenschieber zu tauschen oder zu verkaufen, wobei manch interessantes Stück seinen Besitzer wechselte.
 Rechenschieberbörse bei der IM 2001
Rechenschieberbörse bei der IM 2001
 Klaus Przadka, Irene Dennert und Dieter von Jezierski im Gespräch
Klaus Przadka, Irene Dennert und Dieter von Jezierski im Gespräch
Das Internet hat auch für die Rechenschiebersammler neue Möglichkeiten gebracht. Auf eigenen Homepages werden Rechenschieber ausgestellt, bei ebay wird damit gehandelt und bei Yahoo gibt es seit einiger Zeit ein Diskussionsforum. Dabei sind vor allem besondere und seltene Stücke interessant, die ich hier vorstellen möchte. Die Bilder davon können auf den jeweiligen Seiten angesehen werden.
Rechenschieber der Firma Tavernier Gravet, Frankreich
Auffällig ist der Metallläufer, der in dieser Form erst von Mannheim erfunden wurde. Der Rechenschieber stammt vermutlich noch aus dem späten 19.Jahrhundert.
http://www.sliderules.clara.net/collection/nonstandard/0007-tavgrav.htm
Rechenschieber von A.W.Faber (später Faber-Castell), Typ 360, ca. 1905
Dieser Rechenschieber ist aus Holz gefertigt, besitzt aber bereits ein Celluloidfurnier.
http://www.hh.schule.de/metalltechnik-didaktik/users/luetjens/rechenschieber/schule/rs10.htm
Spezialrechenschieber für Berechnungen bei Warmwasserboilern. Hergestellt von H.W. Healy in London, 1923. Das Material ist Mahagoniholz mit Celluloidauflage. (Zubehör: Aufbewahrungsschachtel, Tabellen)
http://www.priscus.co.uk/acatalog/Priscus_Special_Application_2.html
Moderner Zweiseitenrechenschieber: Faber-Castell 2/83N Novo-Biplex
Der Rechenschieber hat insgesamt 30 Skalen!
http://www.sphere.bc.ca/test/nib.html
Demonstrationsrechenschieber aus der JTG-Physiksammlung: Diese Modelle wurden an die Tafel gehängt und hatten zum besseren Ablesen extra dicke Skalenstriche.
Aristo Nr. 3/150 (Länge über 1,5m!)

Faber Castell Schulstab Log-Log (Länge ca. 1,30m)

Hier noch einige Beispiele für Geräte, denen ebenfalls ein logarithmischer Aufbau zugrunde liegt, die aber keine geradlinigen durchgehenden Skalen wie der Rechenschieber besitzen:
Rechenscheibe: Auf ihr sind die Skalen kreisförmig angeordnet, ansonsten funktioniert sie genau wie ein Rechenschieber.
Hier ein Modell der Firma Gilson/Florida, ca. aus dem Jahr 1940, aus Aluminium. Auf Vorder- und Rückseite sind insgesamt 21 Skalen angebracht.
http://www.sphere.bc.ca/test/circular.html
Rechenwalze: Loga-Walze, 1930
Durch zylinderförmige Anordnung der Skala erreicht man bei einem Durchmesser von 16cm eine Skalenlänge von 15m und damit enorme Genauigkeit!
http://home.t-online.de/home/jan.meyer/rechnsch.htm
Eine Besonderheit ist auch der „Otis King´s Pocket Calculator“: Auf ihm sind die Skalen spiralförmig aufgebracht, und können ineinander geschoben werden. Der Läufer wird durch das schwarze Rohr ersetzt, das wiederum über beiden Skalen gleiten kann.
Zusammengeschoben ist dieses Gerät nur 15cm groß, hat aber die stattliche Skalenlänge von 1,6m! Hergestellt in London, ca. 1960.
http://dicklyon.home.mindspring.com/OK/OK4sale.jpg
Eher ein Scherzartikel ist diese Rechenschieber-Krawattennadel (Länge ca. 5 cm)
http://www.eyrie.org/~dvandom/slide/slidegallery.html
Ebenfalls etwas amüsant ist der Belt-Carrier, der von Keuffel&Esser für seine Modelle angeboten wurde. Damit musste man keine eigene Tasche mehr für den Rechenschieber mitführen sondern konnte ihn sich praktischerweise gleich an den Gürtel schnallen.
http://www.spdc.com.au/sr/Keuffel&Esser/K&ECatalogs/1972/1972kecatp14.htm
Diese Erfindung erinnert schon fast an die Grafik im Kapitel I und zugleich an unsere heutige Zeit: Der Rechenschieber wird nicht versteckt sondern außen am Gürtel getragen, genau wie das Handy; man muss ja zeigen, wer man ist….
Trotz dieser einfallsreichen Ideen kam bedauerlicherweise das unwiderrufliche Aus für das „Werkzeug des Ingenieurs“ und den „Liebling von Millionen“. Aus anderer Sicht dagegen ist sein Ende nicht zu bedauern: Der Rechenschieber trägt nämlich auch den Beinamen „Alptraum mancher Schüler“(62). Wie man selbst darüber denken mag, bleibt jedem selbst überlassen. Irene Dennert hat es einfach so formuliert: „Alles hat seine Zeit“.(63)
Fußnoten:
1 aus: Marks, Seite 11
2 aus: Jezierski, Seite 18
3 aus: http://www-history.mcs.st-andrews.ac.uk/history/Bookpages/Napier10.jpeg
4 aus: Horsburgh, Section A, Seite 4
5 aus: Horsburgh, Section A, Seite 3
6 „Beschreibung des wunderbaren Kanons der Logarithmen“, Übers. d. Verf.
7 aus: http://www.micheloud.com/FXM/sprites/Tabel1620b.gif
8 aus: Horsburgh, Section A, Seite 12
9 frei nach: http://www-math.sci.kun.nl/math/werkgroepen/gmfw/bronnen/napier1.html
10 aus: http://www-math.sci.kun.nl/math/werkgroepen/gmfw/bronnen/napier1.html
11 aus: Jezierski, Seite 2
12 aus: Horsburgh, Section A, Seite 13
13 aus: Horsburgh, Section A, Seite 14
14 aus: Benton, Band 16, Seite 77
15 aus: Jezierski, Seite 3
16 aus: Jezierski, Seite 4
17 aus: Jezierski, Seite 4
18 aus: Jezierski, Seite 4
19 aus: Jezierski, Seite 4
20 Grafik aus: http://www.oughtred.org/oughtred.html
21 vgl. Jezierski, Seite 7 und Horsburgh, Section F, Seite 155
22 vgl. Horsburgh, Section F, Seite 155
23 aus: Horsburgh, Section F, Seite 163
24 aus: Horsburgh, Section F, Seite 165
25 aus: Jezierski, Seite 9
26 aus: Jezierski, Seite 10
27 aus: Jezierski, Seite 38
28 Mantisse: Zahl x = m • Be (B meist 10, 1 m < 10, selten auch 0m<1); m wird dabei Mantisse, Be Kennzahl genannt
nach: Athen/Bruhn
29 aus: Dennert & Pape KG, Seite 9
30 aus: Rechenstamm, Seite 77
31 aus: Jezierski, Seite 38
32 aus: Marks, Seite 105
33 aus: Barth, Mühlbauer, Nikol, Wöhrle, Seite 18
34 frei nach: von Rechenstamm, Seite 76/77
und: Bachmann, Seite 17-19
35 aus: Jezierski, Seite 11
36 aus: Jezierski, Seite 10
37 aus: Jezierski, Seite 15
38 aus: Jezierski, Seite 15
39 aus: Jezierski, Seite 10
40 aus: Jezierski, Seite 16
41 aus: Jezierski, Seite 40
42 aus: Jezierski, Seite 33
43 aus: Jezierski, Seite 18
44 aus: Craenen, Seite 119
45 aus: Jezierski, Seite 15
46 aus: Craenen, Seite 120
47 aus: Jezierski, Seite 47
48 aus: Jezierski, Seite 27
49 aus: Jezierski, Seite 38
50 aus: Jezierski, Seite 38
51 aus: Jezierski, Seite 39
52 aus: Jezierski, Seite 32
53 aus: Craenen, Seite 126
54 aus: Dennert, Seite 103
55 aus: Jezierski, Seite 32
56 aus: Craenen, Seite 127
57 aus: Dennert, Seite 104
58 aus: Jezierski, Seite 77
59 aus: http://www.slideruleguy.com/
60 aus: http://www.sliderule.ca/
61 aus: http://www.oughtred.org/
62 aus: Jezierski, Seite 91
63 aus: Dennert, Seite 104
Quellenverzeichnis
verwendete Literatur:
Athen/Bruhn: „Lexikon der Schulmathematik“ (Band 2)
Weltbild Verlag; Augsburg; 1993
Bachmann, Harald: „Auflösung quadratischer Gleichungen mit dem Rechenstab“ (Seite 17-19)
in: A.W. Faber-Castell (Hrsg): „Rechenstabbrief 1/61“
Selbstverlag; Stein bei Nürnberg; 1961
Barth, Mühlbauer, Nikol, Wöhrle: „Mathematische Formeln und Definitionen“
Bayerischer Schulbuch-Verlag, J. Lindauer Verlag (Schaefer); München; 7. Auflage 1998
Benton, William (Hrsg): „Encyclopaedia Britannica“ (Volume 16)
London, Chicago, Geneva, Sydney, Toronto; 1768/1963
Craenen, Guus: „Albert Nestler: Innovation und Qualität“ (Seite 119-135)
in: Konrad-Klein, Kühn, Petzold (Hrsg): „7. Internationales Treffen für Rechenschieber- und Rechenmaschinensammler – IM2001“ (Tagungsbroschüre)
Dennert, Irene: „ARISTO – Rechenstabfertigung in Bayern“ (Seite 101-104)
in: Konrad-Klein, Kühn, Petzold (Hrsg): „7. Internationales Treffen für Rechenschieber- und Rechenmaschinensammler – IM2001“ (Tagungsbroschüre);
München; August 2001
Daemen-Schmid, H.: „Anleitung zum Gebrauch des Loga-Calculators“
Loga-Calculator; Zürich; ohne Jahresangabe
Dennert & Pape KG (Hrsg): „Anleitung zum Rechenstab Aristo Rietz 89, 99, 109“; Hamburg; 1955
Horsburgh, E. M.: „Handbook of the Exhibition of Napier Relicts and of books, instruments, and devices for facilitating Calculation“
The royal society of Edinburgh, G. Bell and Sons; Edinburgh; 1914
Jezierski, Dieter von: „Rechenschieber – eine Dokumentation“
Eigenverlag; Stein; 1997
Marks, Robert W.: „Rechenschieber – Schritt für Schritt“
Humboldt-Taschenbuchverlag; München; 1972
Rechenstamm, Dr. Lothar Schrutka Edler von: „Theorie und Praxis des Logarithmischen Rechenschiebers“
Verlag Franz Deuticke; Leipzig und Wien; 2. Auflage 1929
verwendete Internetadressen:
Inhaltlich zitiert:
http://www.sliderule.ca/
http://www-math.sci.kun.nl/math/werkgroepen/gmfw/bronnen/napier1.html
Bilder/Grafiken verwendet:
http://amug.org/~puppy/
http://dicklyon.home.mindspring.com/OK/OK4sale.jpg
http://home.t-online.de/home/jan.meyer/rechnsch.htm
http://www.calculators.de/index.htm
http://www.eyrie.org/~dvandom/slide/slidegallery.html
http://www.hh.schule.de/metalltechnik-didaktik/users/luetjens/rechenschieber/schule/rs10.htm
http://www.micheloud.com/FXM/sprites/Tabel1620b.gif
http://www.oughtred.org/
http://www.oughtred.org/oughtred.html
http://www.priscus.co.uk/acatalog/Priscus_Aristo_51.html
http://www.priscus.co.uk/acatalog/Priscus_Special_Application_2.html
http://www.sliderule.ca/Mannheim.jpg
http://www.sliderule.de/body_historie.htm
http://www.slideruleguy.com/
http://www.sliderules.clara.net/collection/nonstandard/0007-tavgrav.htm
http://www.spdc.com.au/sr/Keuffel&Esser/K&ECatalogs/1972/1972kecatp14.htm
http://www.sphere.bc.ca/test/circular.html
http://www.sphere.bc.ca/test/nib.html
http://www.sphere.bc.ca/test/used.html
http://www.tcocd.de/Pictures/SlideRules/Aristo/nr99.html
http://www.tcocd.de/Pictures/SlideRules/SlideRules.html
http://www-history.mcs.st-andrews.ac.uk/history/Bookpages/Napier10.jpeg
http://www-math.sci.kun.nl/math/werkgroepen/gmfw/bronnen/napiertabellen.html
http://www-ppg.dcs.st-and.ac.uk/Languages/Napier88/JohnNapier/
verwendete Software:
Der Rechenschieber, Version 1.0.1
geschrieben von Th. Fichtenkamm, Frühjahr 2000
Downloadadresse: http://62.146.24.196/softwarepage/
Rechenschieber, Version 3.2
Peter Holland, Dezember 2000
Downloadadresse: http://www.peterholland.de/
Windows Slide Rule Model 640
SLG Data Systems and Analysis, 1995
31950 Pembroke Court, Delmar MD 21875
Downloadadresse: http://www.sphere.bc.ca/test/srsoftware.html
