Johann – Sebastian – Bach – Gymnasium Windsbach
Kollegstufenjahrgang 1999/2001
Facharbeit im Fach Mathematik
„Der Rechenschieber und seine Funktionsweise“
Verfasser: Hannah Dürr
Abgabetermin: 01. Februar 2001
Inhaltsverzeichnis:
1. Der Rechenschieber – eine wichtige Rechenhilfe der Vergangenheit
2. Der Rechenschieber – Geschichte, Aufbau und Umgang
2.1. Die Geschichte des Rechenschiebers
2.1.1. Erste Entwicklungen in England
2.1.1.1. Entwicklung der Logarithmen
2.1.1.2. Erste Entwicklung der logarithmischen Skala
2.1.1.3. Entwicklung einer kongruenten Skala
2.1.1.4. Erste Benutzung eines Doppelseiten–Rechenschiebers
2.1.2. Weitere Entwicklungen in anderen europäischen Ländern
2.1.2.1. Vorstellung eines neuen Skalensystems in Frankreich
2.1.2.2. Erste Herstellung eines Rechenschiebers in Deutschland
2.1.2.3. Verbreitung des Rechenschiebers in den USA
2.1.2.4. Weitere Verbreitung des Rechenschiebers vor allem im 20. Jahrhundert
2.2. Die mathematischen Grundlagen des Rechenschiebers
2.2.1. Einführung in die Logarithmen
2.2.1.1. Begriffe und Grundformen
2.2.1.2. Rechenregeln für das Logarithmieren
2.2.2. Prinzip des Rechenschiebers
2.3. Rechnen mit dem Rechenschieber
2.3.1. Grundlagen des Rechenschiebers – Grundbegriffe und Einstellungen
2.3.2. Das Multiplizieren
2.3.3. Das Dividieren
2.3.4. Potenzieren und Wurzelziehen
2.3.5. Das Rechnen mit versetzten Skalen
3.Heute wird der Rechenschieber kaum noch verwendet
1. Der Rechenschieber – eine wichtige Rechenhilfe der Vergangenheit
„Ein Mann, der recht zu wirken denkt,
Muß auf das beste Werkzeug halten.“
Das läßt Goethe in „Faust – Der Tragödie erster Teil“ schon den Direktor sagen.
Das beste Werkzeug der Mathematiker war für mehr als 3 Jahrhunderte der Rechenschieber, bis er vor ca. 25 Jahren vom Taschenrechner abgelöst wurde und schon bald darauf praktisch vergessen war. „Es ist erstaunlich, wie schnell der Rechenschieber nach der Erfindung des Taschenrechners in der Mathematik verschwand.“ Das liegt vor allem daran, dass viele nicht mehr mit dem Rechenschieber umgehen können, was durch die Leichtigkeit, mit einem Taschenrechner zu rechnen, verstärkt wird.

Abb.1 Karikatur
Doch vor dem Auftreten der Elektronik war der Rechenschieber von großer Bedeutung und ein erstaunliches Gerät. Für alle mathematischen Berechnung durfte er nicht fehlen und „um 1940 herum trugen Ingenieure in den Vereinigten Staaten ihren Rechenschieber wie Offiziere ihren Degen oder ein Cowboy seinen Colt“ Die Bedeutung des Rechenschiebers wird durch solche Äußerungen annähernd erläutert.
2. Der Rechenschieber – Geschichte, Aufbau und Umgang
2.1. Die Geschichte des Rechenschiebers
2.1.1. Erste Entwicklungen in England
2.1.1.1. Entwicklung der Logarithmen
Die Erfindung des Rechenschiebers ist eng verbunden mit der Geschichte des Logarithmus, da er auf diesem aufbaut. Als Entdecker des Logarithmus und dessen Berechnung wird in der Literatur der Gutsbesitzer Lord John Napier, Baron of Merchiston, (1550 – 1617) genannt. Der Engländer veröffentlichte 1614 in der Schrift „Mirifici logarithmorum Canonis Descriptio“, die „Wunderbaren Regeln der Logarithmen“, die erste Logarithmentafel, die er innerhalb von fast 20 Jahren errechnet hatte. Jedoch gebührt dem Mechaniker und Astronom Jost Bürgi (1552 – 1632) eine mindestens genauso große Ehre, da der Schweizer unabhängig von Napier bereits 1603 – 1611 eine Logarithmentafel errechnet hatte, sie aber erst 1620 veröffentlichte. Doch blieb die Logarithmentafel von Napier nicht lange unverändert, denn schon kurz nach dessen Veröffentlichung legte Henry Briggs (1561 – 1630) dem Logarithmus die Basis 10 zugrunde. Daher wird der dekadische Logarithmus auch Briggs’scher Logarithmus genannt. Briggs, Professor in Gresham, erweiterte die Logarithmentafel im Jahr 1624 auf 14 Stellen. Letztlich vervollständigt wird die Tafel jedoch erst 1628 von dem Holländer Adrian Vlacq. Edmund Gunter (1581 –1626) trug ebenfalls zur Weiterentwicklung des Logarithmus seinen Teil bei, da er 1620 eine Tafel für Sinus und Tangens errechnete.
1619 wurde der Theologe Gunter Professor für Astronomie am Gresham College, wo er Kollege von Briggs und William Oughtred (1575 – 1660), einem Professor für Mathematik wurde.
2.1.1.2. Erste Entwicklung der logarithmischen Skala
Edmund Gunter wurde wegen einer anderen mathematischen Idee berühmt. Ebenfalls im Jahre 1620 setzt er die logarithmischen Zahlenwerte in die graphische Form einer Strecke um, was die Grundlage für den späteren Rechenschieber war. Als Jahr der Erfindung des Rechenschiebers wird auch 1624 genannt. Edmund Wingate (1595 –1660) führte in diesem Jahr die so genannte Gunter–Skala in Frankreich ein. Sie ermöglichte das Multiplizieren und Dividieren mittels dieser Skala und eines Stechzirkels. Sie „war ein Lineal aus Buchsbaumholz von ca. 60 cm Länge […] und ca. 5 cm Breite […] mit einseitig abgeschrägter Kante. Auf Vorder- und Rückseite waren logarithmische und dezimale Skalen aufgetragen“. Das Arbeiten mit einem Stechzirkel war langwierig und umständlich. „Multiplizierte man z.B. 1,97 mit 2,56, steckte man den Zirkel am Anfang der Skala ein, griff die Strecke bis 1,97 ab. Diese Spanne wurde dann nochmals ab 2,56 abgetragen und gab dann an der rechten Zirkelspitze das Ergebnis an.“
2.1.1.3. Entwicklung einer kongruenten Skala
Der Theologe und Mathematiker William Oughtred behob das Problem, als er 1627 die Idee von zwei aneinander gleitenden Skalen in die Tat umsetzte. Kurze Zeit später führte Edmund Wingate diese „Rule of proportion“ von Oughtred in Frankreich ein. 1654 baute Robert Bissaker den ersten Rechenschieber mit beweglicher Zunge in einem Stabkörper, der durch Messinghalterungen verbunden war. Der Rechenschieber hatte 19 verschiedene Skalen, die von der Gunter–
Skala abgeleitet waren. Drei Jahre später (1657) erfand Seth Patridge (1603–1686) den Urtyp des Doppelseiten–Rechenschiebers, der in London von Walter Haynes gebaut wurde.
2.1.1.4. Erste Benutzung eines Doppelseiten–Rechenschiebers
Den Hauptnutzen aus dem Gebrauch des Rechenschiebers zog zu Beginn vor allem die Seefahrt. Das neu Gerät wurde beim Bau von Schiffen, für Berechnungen von Frachtgütern und im kaufmännischen Bereich benutzt.
Für James Watt (1736 – 1819) war er für die Konstruktion der Dampfmaschine, vor allem zur Festlegung der Maße, von großer Bedeutung. Watt legte einen neuen Meilenstein, als er mit dem Mathematiker Southern, einer seiner Mitarbeiter, einen Rechenschieber für Ingenieure und Techniker entwickelte, um deren Arbeit zu erleichtern. Handwerker stellten auch die ersten Prototypen in Watts Fabrik her. Die „SOHO-rules“ von James Watt wurden als erste technische Rechenschieber in England weit verbreitet und setzten ab ca. 1775 neue Maßstäbe in Qualität und Anordnung der Skalen.
2.1.2. Weitere Entwicklung in anderen europäischen Ländern und in den USA
Erstmals mit der Maschine gefertigt wurde der Rechenschieber von der französischen Firma Lenoir im Jahr 1821. Diese Firma war auch in der ersten Hälfte des 19. Jahrhunderts der führende Hersteller weltweit. Der Rechenschieber wurde durch die industrielle Fertigung weit verbreitet und Mitte des 19. Jahrhunderts war in Frankreich, Italien und Österreich-Ungarn das Rechnen mit dem Rechenschieber bereits an den Schulen empfohlen.
2.1.2.1. Vorstellung eines neuen Skalensystems in Frankreich
Mitte des 19. Jahrhunderts erhielt das System des Rechenschiebers in Frankreich jene Gestalt, das im Prinzip bis in die Gegenwart verwendet wird. 1850 stellte Amédée Mannheim sein neues Skalensystem vor. Er nannte die aneinander gleitenden Grundskalen A!B und C!D. Außerdem unterteilte er das obere Skalenpaar A!B von 1 – 100 und das untere C!D von 1 – 10. Den Sinus und Tangens setzte er auf die Rückseite der Zunge. Zur Erleichterung des Ablesens griff er die Idee des Läufers wieder auf, nachdem 1775 John Robertson (1712 – 1776), Professor für Mathematik ihn schon einmal vorgestellt hatte, er sich aber nicht durchgesetzt hatte.
2.1.2.2. Erste Herstellung eines Rechenschiebers in Deutschland
In Deutschland wurde der Rechenschieber erst viel später bekannt. G. F. Brander aus Augsburg (1713 – 1783), einer der berühmtesten Instrumentenbauer seiner Zeit, stellte als erster deutscher Handwerker einen Rechenschieber her. Aber erst Ende des 19. Jahrhunderts gab es eine Inlandsproduktion von den Firmen wie Dennert & Pape, A. W. Faber, Nestler und Reiss. Damit war Deutschland eines der letzten Länder Europas, die Rechenschieber produzierten. Jedoch verschafften die hohe Qualität und die ständigen konstruktiven Verbesserungen den deutschen Produkten bald einen guten Weltruf.
2.1.2.3. Verbreitung des Rechenschiebers in den USA
In den USA blieb der Rechenschieber noch lange Zeit unüblich. Erst als William Cox das System Mannheims ab 1890 in den „Engineering News“ einführte, wurde das moderne Rechengerät bekannter. Cox ließ sich die Patente geben für den Standard–Rechenschieber des Mannheim–Systems. Später produzierte die Firma Keuffel & Esser die Mannheim–Modifikationen. Zuvor schon verkaufte die Firma die Modelle von Dennert & Pape.
2.1.2.4. Weitere Verbreitung des Rechenschiebers vor allem im 20. Jahrhundert
Der Rechenschieber wurde durch verschiedene Spezialisierungen weiter verbreitet. John Robertson etwas setze die Gunter–Skala so für nautische Berechnungen um, dass auch in der Seefahrt auf den Stechzirkel weitgehend verzichtet werden konnte. Leopold Karl Schulz von Straßnitzki (1802 – 1852) hielt zahlreiche Vorlesungen vor verschiedenen Zielgruppen in Österreich–Ungarn, um den Rechenschieber vor allem im Handwerkerstand publik zu machen. Dazu benutzte er den ersten Demonstrations–Rechenschieber. Ein weiterer Protagonist war Rudolf Mehmke, der einen Rechenschieber für Chemiker erfand.
Zusammenfassend läßt sich feststellen, dass die Entwicklung des Rechenschiebers zwei Jahrhunderte durch englische Mathematiker bestimmt war, bevor ab 1850 ein halbes Jahrhundert Frankreich den Markt des Rechenschiebers beherrschte. Vom 20. Jahrhundert an übernahmen deutsche Hersteller die Führung bei der Produktion und bauten eine gewisse Vorrangstellung aus.
2.2. Die mathematischen Grundlagen des Rechenschiebers
2.2.1. Einführung in die Logarithmen
2.2.1.1. Begriffe und Grundformen
Wie schon gezeigt, wurde der Rechenschieber erst nach der ersten Logarithmentafel erfunden. Dies liegt daran, dass der Rechenschieber auf den Logarithmen aufbaut. Um das Prinzip des Rechenschiebers zu verstehen, müssen zunächst der Logarithmus und seine Rechenregeln begriffen worden sein. Dazu ist es notwendig, mit den Grundbegriffen umgehen zu können.
Dies wird an folgendem Beispiel gezeigt: a = bn
b ist Grundzahl oder Basis
n ist die Hochzahl oder Potenz
a ist die potenzierte Grundzahl
• a nennt man Quadratzahl, wenn n = 2
• a nennt man Kubikzahl, wenn n = 3
Wenn man n errechnen will, so muss man die Gleichung folgendermaßen umformen: n = logba
Hierbei wird a als Numerus oder Logarithmand bezeichnet und n als Logarithmus der Zahl a zur Basis b.
Wenn man die erste Gleichung in die zweite einfügt, erhält man n = logbbn.
Hat man einen Logarithmus zur Basis 10, so handelt es sich um einen dekadischen oder Briggs’schen Logarithmus.
„Die Ziffer des Logarithmus, die vor dem Komma steht, heißt Kennziffer; die Ziffernfolge hinter dem Komma wird Mantisse genannt.“ Logarithmen mit gleicher Ziffernfolge, aber verschiedenem Stellenwert, haben die gleiche Mantisse, aber verschiedene Kennziffern. Dies ist an einem Beispiel leicht zu erkennen:
log101,81 = 0,2577
Aber mit anderem Stellenwert ergibt sich:
log10181 = 2,2577
In Logarithmentafeln werden meist nur die Mantissen angegeben, da die Kennziffer leicht zu bestimmen ist. Die Kennziffer ergibt sich aus der Stellenzahl des Numerus vor dem Komma, die um eins vermindert wird. Das ist am bekannten Beispiel abzulesen:
log10181 (drei Ziffern) = 2,2577
2.2.1.2. Rechenregeln für das Logarithmieren
Es gibt vier wichtige Rechenregeln für den Logarithmus, auf denen sowohl jegliches Rechnen mit dem Logarithmus als auch der Rechenschieber beruht.
1. logb(u – v) = logbu + logbv
d.h.: Der Logarithmus eines Produktes ist gleich der Summe der Logarithmen der Faktoren.
2. logb(u : v) = logbu – logbv
d.h.: Der Logarithmus eines Quotienten ist gleich der Differenz aus dem Logarithmus des Dividenden minus dem Logarithmus des Divisors.
3. logb(un) = n – logbu
d.h.: Der Logarithmus einer Potenz ist gleich dem Produkt aus dem Exponenten und dem Logarithmus der Grundzahl.
4. logbn√u = a logbu
d.h.: Der Logarithmus einer Wurzel ist gleich dem Quotienten aus dem Logarithmus des Radikanden durch den Wurzelexponenten
2.2.2. Prinzip des Rechenschiebers
Durch die Rechenregeln ergibt sich, dass der Logarithmus eines Produkts durch die Summe der Mantissen der Logarithmen der Faktoren bestimmt werden kann und der Stellenwert durch eine Überschlagsrechnung. Führt man dies weiter, kann man auch zu einem Ergebnis kommen, wenn man die Strecken der Mantissen aneinanderreiht und die Gesamtlänge misst. Auf diesem Prinzip beruht der Rechenschieber. Auf ihm sind Mantissen als Strecken aufgetragen. Da die Mantissen mit der Größe des jeweiligen Numerus ungleichmäßig anwachsen, entsteht ein Maßstab mit ungleichmäßiger Teilung. Durch den Logarithmus ergibt sich auch, dass der Rechenschieber mit 1 beginnt. Denn log101 hat den Wert 0.
Für das Rechnen mit dem Rechenschieber gelten die gleichen Regeln wie für das Rechnen mit dem Logarithmus. Die erste Regel bezieht sich auf das Multiplizieren, denn diese wird als Addition ausgeführt. So zieht jede Streckenverlängerung eine Multiplikation mit sich. Nach dem gleichen Prinzip wird das Dividieren als Differenz ausgeführt. Daher ergibt auch jede Streckenverkürzung eine Division. Bei zwei gleichen Skalen, die gegeneinander verschoben sind, wird beim senkrechten Übergang von einer Skala auf die andere multipliziert beziehungsweise dividiert. Ebenso ist bekannt, dass das Verdoppeln eines Logarithmus den Numerus quadriert, verdreifacht man einen Logarithmus, erhebt man den Numerus in die dritte Potenz. Daraus folgt, dass man für das Potenzieren eine Mantissen–Strecke mal nehmen muss. Weil sich die Mantissen bei gleicher Ziffernfolge, aber verschiedenen Stellenwert des Numerus wiederholen, ist auf dem Rechenschieber nur die Ziffernfolge von Bedeutung. Der Stellenwert muss durch eine Überschlagsrechnung in einer Hilfsrechnung ermittelt werden.
2.3. Rechnen mit dem Rechenschieber
2.3.1. Grundlagen des Rechenschiebers – Grundbegriffe und Einstellungen
Bevor man das Rechnen mit dem Rechenschieber erlernen kann, sollte man einige Grundbegriffe kennen. Der Rechenschieber besteht aus drei Teilen, aus dem Stabkörper, dem Läufer und der Zunge. (Abb. 2)
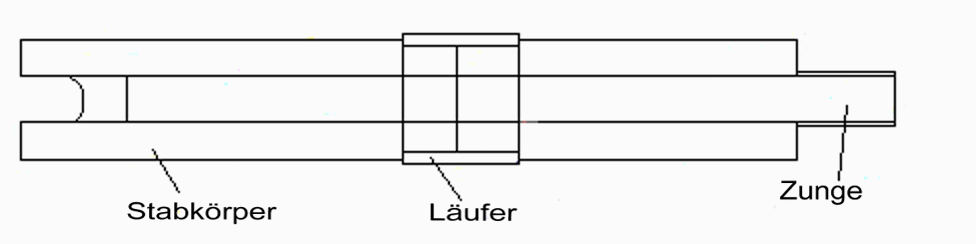
Abb.2 Die Teile des Rechenschiebers
Die Skalen C und D haben die gleiche Unterteilung, wobei sie sich vom normalen Maßstab unterscheiden, da sie ungleichmäßig geteilt sind. (Siehe S. 12)
Es ist notwendig, die richtige Unterteilung zu kennen und ablesen zu können. Auf der D– und C–Skala ist die Unterteilung zwischen 1 und 2 in Zehntel und Hundertstel, zwischen 2 und 3 in Zehntel und diese nur noch in 5 Teile untergliedert und zwischen 4 und 10 sind die Zehntel nur noch halbiert, Zwischenwerte müssen geschätzt werden. Es ist sehr wichtig, dass der Stellenwert der Ziffern nicht berücksichtigt wird, sondern nur die Ziffernfolge. So wird zum Beispiel die Zahl 1710 ebenso eingestellt wie die Zahl 1,710. Die Zahlen werden durch den Anfangsstrich der C–Skala (C1) eingestellt. Die Zunge wird so weit nach rechts geschoben bis C1 auf den Wert auf der D–Skala zeigt.
Bei den Grundrechenarten gilt die Regel:
feste Skala – bewegliche Skala – feste Skala
2.3.2. Das Multiplizieren
Die einfachste Rechenart, die auf dem Rechenschieber ausführbar ist, ist das Multiplizieren. Da nur die Ziffernfolge bestimmt wird, erleichtert es den Rechengang, wenn man zuerst ein ungefähres Ergebnis mit gerundeten Zahlen bestimmt (Überschlagsrechnung). Das Rechnen geschieht stets nach dem folgenden Schema.
Abb. 3 Multiplikation auf dem Rechenschieber
bedeutet die Addition zweier Stecken
Zuerst wird C1 an den ersten Faktor (hier: 24) auf der D–Skala angelegt (Abb. 4).

Abb. 4 C1 wird an den ersten Faktor (2-4-0) gelegt
Hierauf wird der Läufer oder besser gesagt der Hauptstrich auf dem Läufer, auf den zweiten Faktor (hier: 38) der C–Skala geschoben und das Ergebnis (hier: 912) unter dem Läuferstrich auf der D–Skala abgelesen (Abb. 5).
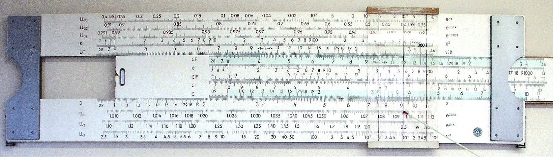
Abb. 5 Unter dem zweiten Faktor (3-8-0) auf der C–Skala ist
das Ergebnis (9-1-2) auf der D–Skala abzulesen
Da oft schon die 3. Stelle schwer abzulesen ist, kann man bei zweistelligen Zahlen die letzte Ziffer durch eine Hilfsrechnung bestimmen, indem man die beiden letzten Ziffern multipliziert. Soll man zum Beispiel 24 – 38 = 912rechnen, so ergibt 4 – 8 = 32 und damit ist die letzte Ziffer, die nicht mehr auf dem Rechenschieber abzulesen ist, als 2 bestimmt worden.

Abb. 6 Durchschieben der Zunge am Beispiel 3-3-0 – 4-1-0 = 1-3-5-3
Kann das Ergebnis nicht abgelesen werden (zum Beispiel: 33 – 41 = 1353 ), weil der zweite Faktor auf der C–Skala über die D–Skala hinausreicht, so muss die Zunge nach vorne durchgeschoben und der Endstrich der C–Skala (C10) auf den ersten Faktor der D–Skala gestellt werden. Der Läufer wird wie gewohnt auf den zweiten Faktor der C–Skala geschoben und das Ergebnis auf der D–Skala unter dem Läuferstrich abgelesen (Abb. 6). Um schon vor der Rechnung festzustellen, ob mit C1 oder C10 eingestellt werden muss, ist wieder eine Hilfsrechnung erforderlich. Es werden die ersten Ziffern der beiden Faktoren miteinander multipliziert und wenn das
Produkt größer als 10 ist, so muss auf jeden Fall mit dem Endstrich eingestellt werden.
2.3.3. Das Dividieren
Das Dividieren ist ähnlich wie das Multiplizieren, nur wird in umgekehrter Reihenfolge vorgegangen. Zuerst wird der Dividend auf der D–Skala mit dem Läufer eingestellt, dann der Divisor der C–Skala unter den Läuferstrich geschoben und das Ergebnis auf der D–Skala unter dem Anfangsstrich der Zunge abgelesen. Ist das Ergebnis nicht unter C1 anzulesen, so steht der Wert unter dem Endstrich der C–Skala.
Möchte man mehrere Rechenvorgänge hintereinander ausführen, so werden die Zwischenergebnisse mit dem Läufer festgehalten und müssen nicht abgelesen werden. Bei kombinierten Rechnungen ist es empfehlenswert, zuerst die Division und dann die Multiplikation auszuführen. Denn je größer die Mantissen werden, desto ungenauer wird die Unterteilung der Zahlen.
2.3.4. Potenzieren und Wurzelziehen
Zum Quadrieren braucht man die D– und die A–Skala; die Zunge ist ohne Bedeutung. Man stellt die Grundzahl mit dem Läufer auf der D–Skala ein und liest das Ergebnis unter dem Läufer auf der A–Skala ab. Die Unterteilung auf der A–Skala ist anders ausgeführt als auf der D–Skala; sie reicht bis 100.
Möchte man die Quadratwurzel errechnen, so läuft das in umgekehrter Reihenfolge ab. Man stellt die Zahl unter der Quadratwurzel auf der A–Skala mit dem Läufer ein und liest auf der D–Skala das Ergebnis ab.
Es muss aber wieder beachtet werden, dass der Rechenvorgang auch hier nur mit der Ziffernfolge ausgeführt wird. Bei Zahlen, die nicht
zwischen 1 und 10 liegen, muss das Komma so verstellt werden, dass links davon nur eine Ziffer steht. Nach dem Ablesen verschiebt sich das Komma bei der Quadratzahl um doppelt so viele Stellen, wie bei der Grundzahl, allerdings in die entgegengesetzte Richtung.
Beispiel: 12,52 – eingestellter Wert 1,252 – Ergebnis auf der A–Skala: 1,5625 – Ergebnis: 156,25
Beim Wurzelziehen wird ebenso verfahren. Bei Zahlen, die kleiner als 1 oder größer als 100 sind, wird das Komma jeweils um 2 Stellen versetzt, bis die Zahl einen Wert zwischen 1 und 100 erreicht. Im Ergebnis muss das Komma um die Hälfte der Stellen zurück verschoben werden.
Kubikzahlen werden mit Hilfe der D– und K–Skala ermittelt. Die K–Skala ist von 1 bis 1 000 unterteilt. Man verfährt wie beim Quadrieren. Die Grundzahl wird mit dem Läufer auf der D–Skala festgehalten und die Kubikzahl auf der K–Skala abgelesen. Sind die Zahlen, die mit 3 potenziert werden sollen, kleiner als 1 oder größer als 10, muss das Komma ebenso wie beim Quadrieren so verschoben werden, dass links von ihm nur noch eine Ziffer steht. Bei der Kubikzahl wird das Komma um 3 mal so viele Stellen nach rechts verschoben. Die dritte Wurzel wird umgekehrt errechnet wie die Kubikzahl. Der Wert wird mit dem Läufer auf der K–Skala eingestellt und die Kubikwurzel auf der D–Skala abgelesen. Sollen aus Zahlen unter 1 oder über 1 000 die dritte Wurzel gezogen werden, so wird das Komma jeweils um 3 Stellen verschoben, bis der Wert zwischen 1 und 1 000 liegt. Beim Ergebnis werden für 3 Stellen des Verschiebens vor der Rechnung jeweils um eine Stelle zurück verschoben.
2.3.5. Das Rechnen mit versetzten Skalen
Vereinfacht wird das Rechnen mit dem Rechenschieber durch die versetzten Skalen. Dazu benötigt man die CF– und die DF–Skala, die nicht auf jedem Rechenschieber zu finden sind. Die beiden Skalen gehen von p (3,14) über 10 bzw. 1 wieder zu p . Die Multiplikation kann ebenso wie bei der C/D–Skalen ausgeführt werden. CF1 wird unter den ersten Faktor auf der festen DF–Skala geschoben, auf der beweglichen CF–Skala wird der zweite Faktor dazu gelegt und das Ergebnis wird über dem zweiten Faktor der CF–Skala auf der DF–Skala abgelesen. Es gilt wie auch schon bei der C– und D–Skala der Dreischritt: von der festen auf die bewegliche Skala und wieder auf die feste. Ebenso sollte für den Stellenwert der Ziffernfolge eine Überschlagsrechnung ausgeführt werden. Es gilt jedoch zu beachten, dass der erste Faktor auf der linken Hälfte der DF – Skala eingestellt werden muss, wenn er größer als p ist.

Abb. 7 Rechnen mit versetzten Skalen (Beispiel 1-7-0 – 3-1-0 = 5-2-7)
Ist das Ergebnis auf der DF–Skala nicht ablesbar, kann man auf die C– und D–Skala wechseln, da C ebenso verschoben wurde wie CF. Folglich ist C10 über dem ersten Faktor auf der D–Skala eingestellt und das Ergebnis auf der D–Skala unter dem zweiten Faktor der C–Skala abzulesen. Durch das kombinierte Verwenden der C/D– sowie der CF/DF–Skalen entfällt das Durchschieben der Zunge bei Zehner–Überschreitungen. Wenn der erste Faktor mit CF1 auf DF eingestellt wird, kann das Ergebnis auf der D– oder DF–Skala abgelesen werden (Abb. 7). Man kann ebenso immer mit der D–Skala beginnen, wobei dann zu beachten ist, dass mit C1 eingestellt werden muss, wenn der Anfangswert (erste Faktor) kleiner als p ist und mit C10, wenn er größer als p ist.
Die DF–Skala ist normalerweise gegenüber der D–Skala um p versetzt, bei kaufmännischen Rechenschiebern jedoch um 3,6. Jeder Wert, der auf der D–Skala mit dem Läufer eingestellt wird, erscheint bei der DF–Skala um 3,14 multipliziert. Somit ist der Kreisumfang leicht auszurechnen, wenn man den Kreisdurchmesser hat und umgekehrt, da Kreisdurchmesser – p = Kreisumfang ergibt.
Ebenso sind die Skalen hilfreich zum Errechnen von dem Flächeninhalt einer Ellipse, der mit der Formel A = a – b – p errechnet wird, wobei a und b gegeben sind.
Auch die Zinsrechnung wird leichter. Hierfür ist aber eine zusätzliche Skala notwendig, die sich auf der Zunge des Rechenschiebers befindet. Sie heißt CI und ist durch ihre roten Zahlen hervorgehoben. Die Rechnung wird folgendermaßen durchgeführt:
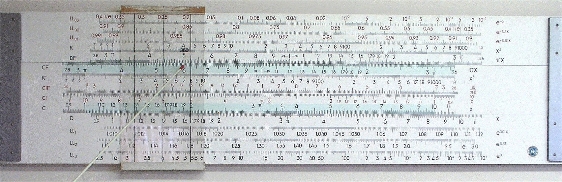
Abb. 8 Einstellen des Kapitals mit dem Läufer–Hilfsstrich
Das Kapital wird mit dem Hilfsstrich rechts neben dem Hauptstrich auf dem Läufer auf der DF–Skala eingestellt. Der Hilfsstrich ist häufig mit „360“ gekennzeichnet. In diesem Beispiel sind 500 Euro als Kapital gegeben (Abb. 8). (Bei kaufmännischen Rechenschieber, deren CF– und DF–Skalen mit 3,6 beginnen, wird der Hauptstrich verwendet.)
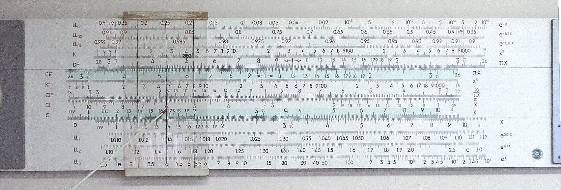
Abb. 9 Zinsfuß wird auf der CI–Skala eingestellt
Der Zinsfluß, hier 6%, wird auf der CI–Skala unter den Läuferhauptstrich geschoben (Abb. 9).

Abb. 10 Einstellen der Tage und Ablesen der Zinsen
Die Tage, in diesem Beispiel 75, werden auf C oder CF mit dem Läuferhauptstrich eingestellt und die Zinsen auf D oder DF abgelesen. Man kommt in diesem Beispiel auf 6,25 Euro Zinsen (Abb. 10). Durch eine Proberechnung kann man das Ergebnis nachprüfen.
Kapital – Zinssatz : 100% – Zinszeit : 360 = Zinsen
500 Euro – 6% : 100% – 75 : 360 = 6,25 Euro
3. Heute wird der Rechenschieber kaum noch verwendet
Dieses erstaunliche Rechengerät wurde jedoch, wie schon genannt, wegen des Taschenrechners schnell vergessen. Heute wird er kaum noch verwendet, da die Elektronik immer weiter entwickelt wird. Es gibt nur wenige Beispielen von alten Ingenieuren wie zum Beispiel Ingenieur Richard Hofmockel aus Wicklesgreuth, die den Rechenschieber weiter verwenden. „Wenn man mit dem Rechenschieber umgehen und rechnen kann, ist er praktischer als ein Taschenrechner, denn mit ihm kann man schneller Kreisdurchmesser oder Winkel errechnen. Außerdem macht es doch einen guten Eindruck, wenn ein Ingenieur mit einem Rechenschieber auf die Baustelle kommt.“ Doch in wiederum 25 Jahren wird es wahrscheinlich den Rechenschieber nur noch im Museum oder unter Sammlern geben. Diese haben wiederum wenig Nachwuchs, weil die neuere Generation mit einem Rechenschieber nichts mehr anzufangen weiß.
Beispiele für Sammlervereine sind der „Circle of the slide rule experts“ oder „The Oughtred Society“, die ein gleichnamiges „Journal“ herausgibt. Es gibt für Rechenschiebersammler ein jährliches Treffen im Deutschen Museum in München, um die Faszination des Rechenschiebers weiterhin zu achten.
Bildverzeichnis:
Abbildung 1: Karikatur
Zeichnung von Tex Rabinowitz aus „Die Zeit“ Nr.19, 06.05.1999. Veröffentlicht auch von R. Schöne unter www-m8.mathematik.tu-muenchen.de/rbg/schoe-ne/komisch/froh/froh.htm am 10.05.1999, aufgerufen am 24.01.01 um 13:09 Uhr
Abbildung 2: Die Teile des Rechenschiebers
vgl. der Abbildung aus „Rechnen mit dem Rechenstab“ S. 11
Abbildung 3: Multiplikation auf dem Rechenschieber bedeutet die Addition zweier Strecken
vgl. der Abbildung aus „Rechnen mit dem Rechenstab“ S. 43
Abbildung 4: C1 wird an den ersten Faktor (2-4-0) gelegt
Eigene Fotografie des Demonstrationsrechenschiebers im Physiksaal des Johann–Sebastian–Bach Gymnasiums Windsbach
Abbildung 5: Unter dem zweiten Faktor (3-8-0) auf der C–Skala ist das Ergebnis (9-1-2) auf der D–Skala abzulesen
Eigene Fotografie des Demonstrationsrechenschiebers
Abbildung 6: Durchschieben der Zunge am Beispiel
3-3-0 – 4-1-0 = 1-3-5-3
Eigene Fotografie des Demonstrationsrechenschiebers
Abbildung 7: Rechnen mit versetzten Skalen
(Beispiel 1-7-0 – 3-1-0 = 5-2-7)
Eigene Fotografie des Demonstrationsrechenschiebers
Abbildung 8: Einstellen des Kapitals mit dem Läufer–Hilfsstrich
Eigene Fotografie des Demonstrationsrechenschiebers
Abbildung 9: Zinsfuß wird auf der CI–Skala eingestellt
Eigene Fotografie des Demonstrationsrechenschiebers
Abbildung 10: Einstellen der Tage und Ablesen der Zinsen
Eigene Fotografie des Demonstrationsrechenschiebers
Literaturverzeichnis:
- Rechenschieber – eine Dokumentation (Geschichte, Hersteller, Modelle) von Dieter von Jezierski
ISBN 3-00-001503-5
Herausgegeben vom Verfasser 1997 im Eigenverlag
Vertrieb: RS – DOKU 97, D. v. Jezierski
Bahnhofstr. 3, D-90547 Stein
- Slide Rules – A Journey through three centuries von Dieter von Jezierski übersetzt durch Rodger Sheherd
ISBN 1-879335-948
Astragal Press, Mendham, NJ
- Interview mit Dieter von Jezierski am 02. Januar 2001
Dieter von Jezierski war 40 Jahre Produkt–Manager für Rechenschieber und Zeicheninstrumente bei Faber–Castell. Er entwickelte mit Mitarbeitern unter anderem den „Novo–Duplex“. Seit 1990 ist er Mitglied des „Circle of slide rule experts“ und veröffentlichte schon mehrere Artikel in dem „Journal of the Oughtred Society“.
vom 24. März 1999, aufgerufen am 27. Dezember 2000
vom 25. Mai 2000, aufgerufen am 27. Dezember 2000
- Mathematik 6, Algebra/Geometrie von Erwin Kunesch und Bernhard Rieck aus dem Bayrischen Schulbuch–Verlag in München, 1.Auflage 1995
- Algebra von Zwerger – Klug, neu bearbeitet von Dr. Walter Zink, 9. Auflage, 1955, J. Lindau Verlag (Schaefer), München
- Basismathematik 10; Algebra; Üben – Verstehen – Anwenden von Christine Penßel, Hans–Jürgen Penßel und Dieter Roth, Ausgabe B; Bayrischer Schulbuch – Verlag, München, 1992, 1. Auflage
- Rechnen mit dem Rechenstab von Gerhard und Charlotte Schröter, Bayreuth
