Rainer Stumpe, Mannheim
Es war eine Idee, die aus dem Geist mehrerer Flaschen Rotwein aufstieg: wie setzt man einen Rechenschieber – wenn man schon einen hat – beim Navigieren auf Segeltörns ein? Der fortgeschrittene Weingenuss brachte uns immerhin noch zur Erkenntnis, Küstennavigation hat etwas mit Dreiecken zu tun, und mit Sinus und Tangens, die ja auf dem Rechenschieber angegeben sind.
Nun hatte ich als Chemiker den Rechenschieber erst vor 20 Jahren mit dem Laborkittel abgelegt, aber eine konkrete Vorstellung hatte ich noch nicht, als ich die Aufgabe übernahm, Vorschläge zu machen. Hilfe kam aus dem Web: ich fand bei Ron Manley Snodgrass‘ „Teach yourself the slide rule“. In dem Buch gibt es ein Kapitel über Navigation. (Die britischen Bomberpiloten benutzten im letzten Krieg den Rechenschieber, um ihre Zielgebiete zu erreichen, und Snodgrass bringt eine Vielzahl der typischen Rechenbeispiele.)
Das Rechenschieberrechnen wurde mir an einem Nachmittag wieder geläufig. Anfangs gab es nur das Problem, den richtigen Ableseabstand mit der Gleitsichtbrille zu finden. Um es kurz zu machen: der Rechenschieber ist ja besonders geeignet für Proportionalitäten (Dreisatzrechnung) und man kann solche Aufgaben schneller als mit dem Taschenrechner lösen. Das heißt, alle Aufgaben im schiefwinkligen Dreieck, die auf dem Sinussatz beruhen, sind mit dem Rechenschieber schnell und leicht zu lösen.
Natürlich ist das Navigieren mit Trigonometrie und dem Rechenschieber nicht leichter als mit GPS und Autopilot. Aber auf unserem letzten Törn waren drei GPS-Geräte ausgefallen (das Bordgerät und zwei Handgeräte). Ich packte also meinen Aristo Studio Rechenschieber aus, in der Hoffnung, Bewunderung zu ernten. Die Reaktion der jüngeren Crewmitglieder war lediglich: „Oh, so sieht ein Rechenschieber aus! Hab‘ schon ‚mal ‚was davon gehört.“. Bei den Begriffen „Sinus“ und „Cosinus“ schwand das Interesse rapide. Eindruck kann man also nicht schinden mit dem Rechenschieber. Es bleibt der Trost, dass der Rechenschieber ein ausgezeichnetes Hirnleistungstrainingsgerät ist.
Geschwindigkeitsberechnung
Die Berechnung der Geschwindigkeit ist eine einfache Divisionsaufgabe – Trigonometrie braucht man nicht. Man rechnet bequem mit den beiden Quadratskalen A und B im oberen Teil moderner Rechenschieber. Beim Rechnen auf diesen beiden Skalen kann man in einer Einstellung mit 60 multiplizieren.
Man stellt einfach die gefahrene Strecke auf der Zungenskala B unter die Fahrtzeit in Minuten auf der Körperskala A und liest unter der 60 der Körperskala A auf der Zungenskala B die Geschwindigkeit in km/h oder Knoten ab – je nach Einheit der Strecke.

Abbildung 1: Berechnung der Geschwindigkeit aus Strecke und Zeit
Im Beispiel (Abbildung 1) ergibt sich die Geschwindigkeit von 7,6 kn aus der Strecke 9,5 sm in 75 min.
Umgekehrt kann man natürlich auch die Zeit berechnen, die man für eine gegebene Strecke bei konstanter Geschwindigkeit brauchen wird. Man stellt die Geschwindigkeit (5,5 kn) auf B unter die „60“ auf A und liest über der Entfernung (3 sm) auf B die benötigte Zeit auf A (knapp 33 min) bis zur Untiefe ab (Abbildung 2).
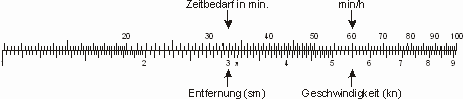
Abbildung 2: Zeitbedarf für eine Strecke bei gegebener Geschwindigkeit
Das schiefwinklige Dreieck und der Sinussatz
Die wirklich interessanten Aufgaben sind die Berechnungen im schiefwinkligen Dreieck. Eine typische Aufgabe ist, den richtigen Kurs bei (Gezeiten-) Strömung zu finden. Die Konstruktion mit Zirkel und Lineal ist recht aufwändig – und bei Seegang nicht gerade einfach (dauernd verschwindet ein Lineal über die Kartentischkante).
Das schiefwinklige Dreieck hat drei Winkel, von denen keiner ein 90°-Winkel ist (sonst wäre es ein rechtwinkliges Dreieck), und in dem keine zwei Seiten gleich lang sind (sonst wäre es ein gleichschenkliges mit 2, oder ein gleichseitiges Dreieck mit 3 gleich langen Seiten).
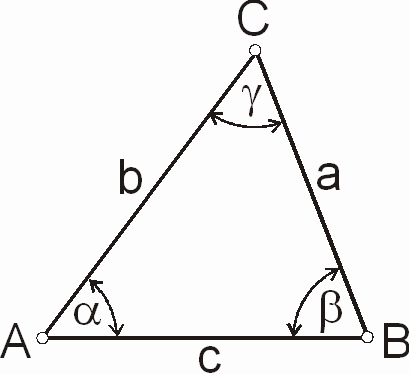
Abbildung 3: Das schiefwinklige Dreieck
In diesem (und in allen anderen Dreiecken) gilt, dass sich die Längen der Seiten a, b und c verhalten wie die Sinuswerte der jeweils gegenüberliegenden Winkel a , b und g :
![]()
Das ist der Sinussatz. Leser in meinem Alter werden in der Schule mit seiner Ableitung vermutlich gelangweilt worden sein, so dass die meisten ihn verdrängt haben. In der Schule ging nämlich völlig unter, was man mit ihm (und dem Rechenschieber) alles Nützliche berechnen kann. Zudem ist er ja einfach genug zu merken.
Ein Dreieck ist durch drei der sechs „Stücke“ eindeutig beschrieben (Stücke sind die drei Seiten und die drei Winkel). Das heißt andrerseits, dass man aus drei gegebenen Stücken die anderen drei berechnen kann. Es gibt da nur die Einschränkung, dass der Sinussatz – der sich für den Rechenschieber am besten eignet – nur anwendbar ist, wenn entweder eine Seite und zwei Winkel gegeben sind, oder zwei Seiten und der einer der Seiten gegenüberliegende Winkel (sonst muss man nach dem Cosinussatz oder dem Tangenssatz rechnen).
Drift in der Strömung
Eines der Probleme für den Navigator ist, den Kurs für den kürzesten Weg zum Ziel zu finden, wenn man quer zur Strömung fahren muss. Je nach Richtung und Geschwindigkeit der Strömung muss man beträchtlich neben das Ziel halten. „Auf Sicht“ gesteuert, oder mit dem GPS nach Zielkoordinaten, beschreibt man einen Bogen. Dabei hat der Segler keine Zeit zu verschenken, denn im Gezeitenrevier muss er ein bestimmtes Ziel zu einer festgelegten Zeit erreichen, weil z. B. sonst der Wasserstand schon zu niedrig ist, um noch in den Hafen zu fahren.
Mathematisch handelt es sich um eine Vektoraddition. Dabei werden zwei Vektoren – die Geschwindigkeit des Bootes und die Geschwindigkeit der Strömung addiert; der resultierende Vektor gibt die Richtung des Steuerkurses an, seine Länge entspricht der Geschwindigkeit, mit der sich das Boot dem Ziel nähert (Abbildung 4).
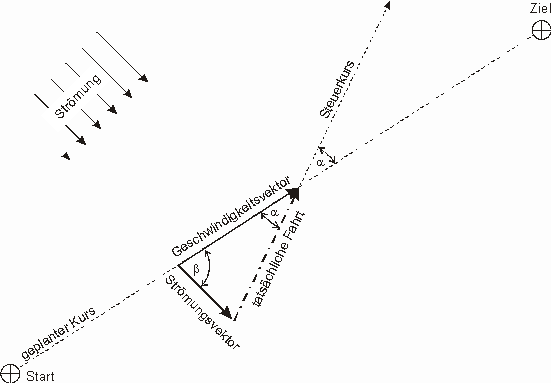
Abbildung 4: Zielaufgabe des Navigators
In dem Dreieck der Abbildung 4 sind bekannt die der Betrag der tatsächlichen Fahrt, die das Boot durch das Wasser macht (= Geschwindigkeit, liest man von der Logge ab, dem „Tacho“ eines Bootes), die Richtung in die man fahren möchte (geplanter Kurs), und Länge und Richtung des Strömungsvektors (entnimmt man dem Strömungsatlas des Seegebietes). Gesucht werden der Winkel a und die Länge des Geschwindigkeitsvektors.
Den Winkel b zwischen Strömungsvektor a und Geschwindigkeitsvektor c kann man berechnen, denn beide Richtungen sind bekannt (sie werden als Winkel zur Nordrichtung angegeben). Wir haben also zwei bekannte Seiten und einen bekannten Winkel, der nicht von den bekannten Seiten eingeschlossen ist: eine Sinussatz-Aufgabe. (Die tatsächliche Fahrt ist der Vektor b, die Seite liegt dem Winkel b gegenüber.)
Nach dem Sinussatz gilt:
![]()
Für den Rechenschieber stürzt man die Formel:
![]()
und stellt auf der Sinusskala den Winkel b ein, stellt darüber die tatsächliche Fahrt (auf der Zungenskala C) und liest unter der 1 (oder 10) der Skala C auf der Sinusskala den Winkel a ab.
Für das Beispiel der Abbildung 4 ist die Strömungsrichtung 135°, die -geschwindigkeit ist 2 kn, die tatsächliche Fahrt beträgt 4 kn (schwacher Wind!), die geplante Kursrichtung ist 57°. Dann ist der Winkel b = 135° – 57° = 78°. Auf dem Rechenschieber sieht das wie in Abbildung 5 aus. Man liest für den Winkel a = 29,4° ab (man kann aber bestenfalls auf volle Grad genau steuern), und muss den Kurs auf 57° – 29° = 28° ändern.
Bleibt noch, die Länge des Geschwindigkeitsvektors c zu berechnen. Wir kennen ja schon zwei Winkel (a und b ), und da die Winkelsumme im Dreieck 180° beträgt, ist der dritte Winkel g = 180° – 78° – 29° = 72°. Mit der Rechenschiebereinstellung zur Berechnung von abrauchen wir nur den Läufer über 72° auf der Sinusskala zu verschieben, und wir können auf D ablesen: 3,85 (kn). Die Strömung bremst uns also, und wir kommen langsamer ans Ziel als unserer Fahrt durch das Wasser entspricht – wenn auch nur wenig. Mit der Methode von oben können wir nun eine Ankunftszeit voraussagen, wenn wir die Entfernung zum Ziel kennen.
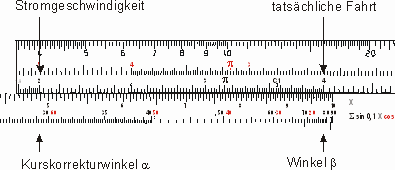
Abbildung 5: Anwendung des Sinussatzes
Ausblick
Versuchen Sie ‚mal, diese Rechnungen mit dem Taschenrechner schneller auszuführen! Mit ein bisschen Rechenschieberübung könnte man hier recht lukrative Wetten abschließen.
Ich denke, diese Beispiele überzeugen, dass man mit ein wenig Trigonometrie und einem Rechenschieber schnell und bequem Navigationsaufgaben lösen kann. Es gibt auch Beispiele, die man vernünftig nur mit Rechenschritten lösen kann (z. B. die Schiffsortbestimmung durch zwei Horizontalwinkel).
Wer mehr wissen will, kann gerne auf meiner Website (www.rainerstumpe.de/HTML/navigation.html) in die Tiefen der Trigonometrie einsteigen – oder mein Buch „Der perplexe Navigator – Navigation mit dem Rechenschieber“ lesen.
Dr. Rainer Stumpe
Neckarpromenade 24
68167 Mannheim
